题目内容
【题目】已知直线y＝kx+b与直线y＝2x+1平行，且过点（1，﹣3）．
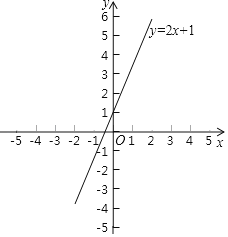
（1）求这个一次函数的关系式？
（2）画出函数图象．
（3）该函数图象与两个坐标轴围成的三角形的面积？
【答案】（1）y＝2x﹣5；（2）如图所示，见解析；（3）该一次函数的图象与坐标轴围成的三角形的面积是
．
【解析】
（1）利用两直线的平行确定比例系数k，再将点（1，
）代入，即可确定解析式；
（2）分别求出该直线与两坐标轴的交点坐标，再过这两个交点画直线即可；
（3）利用三角形的面积公式，即可求得面积.
解：（1）∵直线y＝kx+b与直线y＝2x+1平行，
∴k＝2，
∵直线y＝2x+b过点（1，﹣3），
∴2+b＝﹣3，
∴b＝﹣5，
∴一次函数的解析式为y＝2x﹣5；
（2）∵y＝2x﹣5，
∴当x＝0时，y＝﹣5；
当y＝0时，x＝2.5，
过（0，﹣5）、（
，0）画直线，得到函数y＝2x﹣5的图象，如图所示：
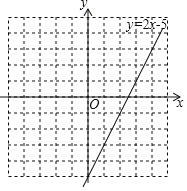
（3）如图，该一次函数的图象与坐标轴围成的三角形的面积是：
.
【题目】阅读下面内容，并按要求解决问题：
问题：“在平面内，已知分别有2个点，3个点，4个点，5个点，…，
个点，其中任意三个点都不在同一条直线上经过每两点画一条直线，它们可以分别画多少条直线？”
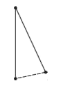
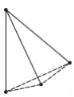
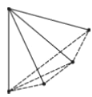
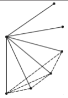
探究：为了解决这个问题，希望小组的同学们，设计了如下表格进行探究：（为了方便研究问题，图中每条线段表示过线段两端点的一条直线）
点数 | 2 | 3 | 4 | 5 | … |
|
示意图 |
|
|
|
| … |
|
直线条数 | 1 |
|
|
| … |
请解答下列问题：
（1）请帮助希望小组归纳，并直接写出结论：当平面内有
（2）若某同学按照本题中的方法，共画了28条直线，求该平面内有多少个已知点？
【题目】某地农产品专卖店收购了一种非常受欢迎的土特产，该店以
元/千克收购了这种土特产
千克，若立即销往外地，每千克可以获利
元．根据市场调查发现，该种土特产的销售单价每天上涨
元/千克，为了获得更大利润，该店决定先贮藏一段时间后再出售．根据以往经验，这批土特产的贮藏时间不宜超过
天，在贮藏过程中平均每天损耗
千克．
（1）若商家将这批土特产贮藏
天后一次性出售，请完成下列表格：
每千克土特产售价(单位：元) | 可供出售的土特产质量(单位：克) | |
现在出售 |
|
|
|
|
|
（2）将这批土特产贮藏多少天后一次性出售最终可获得总利润
元？
