题目内容
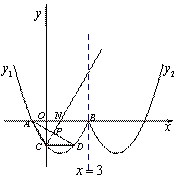
如图,曲线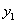 抛物线的一部分,且表达式为:
抛物线的一部分,且表达式为: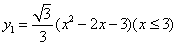 曲线
曲线 与曲线
与曲线 关于直线
关于直线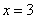 对称。
对称。
(1)求A、B、C三点的坐标和曲线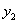 的表达式;
的表达式;
(2)过点D作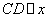 轴交曲线
轴交曲线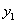 于点D,连接AD,在曲线
于点D,连接AD,在曲线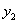 上有一点M,使得四边形ACDM为筝形(如果一个四边形的一条对角线被另一条对角线垂直平分,这样的四边形为筝形),请求出点M的横坐标。
上有一点M,使得四边形ACDM为筝形(如果一个四边形的一条对角线被另一条对角线垂直平分,这样的四边形为筝形),请求出点M的横坐标。
(3)设直线CM与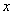 轴交于点N,试问在线段MN下方的曲线
轴交于点N,试问在线段MN下方的曲线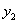 上是否存在一点P,使△PMN的面积最大?若存在,求出点P的坐标;若不存在,请说明理由。
上是否存在一点P,使△PMN的面积最大?若存在,求出点P的坐标;若不存在,请说明理由。
 |
(1)对点A、B、C坐标的意义要明白,点A与点B
是二次函数与横轴的交点,点C是也纵轴的交点
关于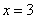 意义的理解,就是将
意义的理解,就是将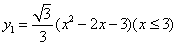
进行了平移。
(2)要理解,只有当CM垂直平分AD时,才能在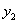 找到点M
找到点M
故点M即为直线(C与AD的中点P连线)的交点
(3)显然MN的值固定,即在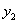 上的点,到CM的距离最大的点,即与CM平行的直线与
上的点,到CM的距离最大的点,即与CM平行的直线与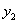 只有一个交点时,即为所求
只有一个交点时,即为所求
 (1)解:易求A(-1,0),B(3,0),C(0,
(1)解:易求A(-1,0),B(3,0),C(0, ),
),

(2)解:若AD垂直平分CM,则可知CDMA为菱形,此时点M(1,0)
显然不在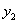 上;故直线CM垂直平分AD,取AD中点P,易求其坐标为
上;故直线CM垂直平分AD,取AD中点P,易求其坐标为
(1, ),故直线CN的解析式为:
),故直线CN的解析式为:
求其与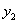 的交点坐标:
的交点坐标:
解之得: ,
, (不合舍去)
(不合舍去)
故
(3)因为MN的长度固定,故点P到MN的距离最大时,△PMN的面积最大
故设:另一直线 与
与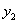 相交于点P,很显然它们只有一个交点时,满足条件。
相交于点P,很显然它们只有一个交点时,满足条件。
即: 只有唯一一个解的时候,这个点就是点P
只有唯一一个解的时候,这个点就是点P
解之得: 
将 代入
代入

故点P的坐标为

 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案某学校举行一次体育测试,从所有参加测试 的学生中随机抽取10名学生的成绩,制作出如下统计表和条形统计图:
的学生中随机抽取10名学生的成绩,制作出如下统计表和条形统计图:
| 编号 | 成绩 |
| 编号 | 成绩 | 等级 |
| ① | 95 | A | ⑥ | 76 | B |
| ② | 78 | B | ⑦ | 85 | A |
| ③ | 72 | C | ⑧ | 82 | B |
| ④ | 79 | B | ⑨ | 77 | B |
| ⑤ | 92 | A | ⑩ | 69 | C |

请回答下列问题:
(1)孔明同学这次测试的成绩是87分,则他的成绩等级是 ;
(2)请将条形统计图补充完整;
(3)已知该校所有参加这次测试的学生中,有60名学生成绩是A等,请根据以上抽样结果,估计该校参加这次测试的学生总人数是多少?
 B.
B.
 D.
D.
 等级
等级 (结果保留π)。
(结果保留π)。

 的一元二次方程
的一元二次方程 有实数根,则
有实数根,则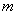 的取值范围是( )
的取值范围是( ) B.
B. C.
C. D.
D.