Question

3．已知：如图，OC是∠AOB的平分线．
（1）当∠AOB=60°时，求∠AOC的度数；
（2）在（1）的条件下，过点O作OE⊥OC，请在图中补全图形，并求∠AOE的度数；
（3）当∠AOB=α时，过点O作OE⊥OC，直接写出∠AOE的度数．（用含α的代数式表示）

Answer 1

分析 （1）直接由角平分线的意义得出答案即可；
（2）分两种情况：OE在OC的上面，OE在OC的下面，利用角的和与差求得答案即可；
（3）类比（2）中的答案得出结论即可．

解答 解：（1）∵OC是∠AOB的平分线（已知），
∴∠AOC=$\frac{1}{2}$∠AOB，
∵∠AOB=60°，
∴∠AOC=30°．
（2）∵OE⊥OC，
∴∠EOC=90°，
如图1，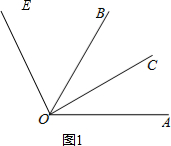

∠AOE=∠COE+∠COA=90°+30°=120°．
如图2，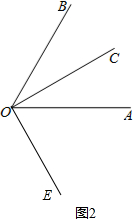

∠AOE=∠COE-∠COA=90°-30°=60°．
（3）∠AOE=90°+$\frac{1}{2}$α或∠AOE=90°-$\frac{1}{2}$α．

点评 此题考查了角的计算，以及角平分线定义，分类考虑，类比推理是解决问题的关键．