题目内容
1. 课本P152有段文字:把函数y=2x的图象分别沿y轴向上或向下平移3个单位长度,就得到函数y=2x+3或y=2x-3的图象.
课本P152有段文字:把函数y=2x的图象分别沿y轴向上或向下平移3个单位长度,就得到函数y=2x+3或y=2x-3的图象.【阅读理解】
小尧阅读这段文字后有个疑问:把函数y=-2x的图象沿x轴向右平移3个单位长度,如何求平移后的函数表达式?
老师给了以下提示:如图1,在函数y=-2x的图象上任意取
两个点A、B,分别向右平移3个单位长度,得到A′、B′,
直线A′B′就是函数y=-2x的图象沿x轴向右平移3个单位长度后得到的图象.
请你帮助小尧解决他的困难.
(1)将函数y=-2x的图象沿x轴向右平移3个单位长度,平移后的函数表达式为C
A.y=-2x+3
B.y=-2x-3
C.y=-2x+6
D.y=-2x-6
【解决问题】
(2)已知一次函数的图象如图2与直线y=-2x关于x轴对称,求此一次函数的表达式.
【拓展探究】
(3)将一次函数y=-2x的图象绕点(2,3)逆时针方向旋转90°后得到的图象对应的函数表达式为y=$\frac{1}{2}$x-$\frac{3}{2}$.(直接写结果)
分析 (1)利用平移规律确定出平移后函数解析式即可;
(2)找出y=-2x上两点坐标,进而求出关于x轴对称点的坐标,利用待定系数法求出一次函数解析式即可;
(3)由题意设出旋转后的函数解析式为y=$\frac{1}{2}$x+b,根据(2,3)到直线y=-2x与y=$\frac{1}{2}$x+b距离相等求出b的值,即可确定出所求函数解析式.
解答 解:(1)利用平移规律得:将函数y=-2x的图象沿x轴向右平移3个单位长度,平移后的函数表达式y=-2(x-3)=-2x+6.
故选:C;
(2)在函数y=-2x的图象上取两个点A(0,0)、B(1,-2),
关于x轴对称的点的坐标A′(0,0)、B′(1,2),
设所求一次函数解析式为y=mx,
把x=1,y=2代入得:m=2,
则一次函数的表达式为y=2x;
(3)设旋转后的函数解析式为y=$\frac{1}{2}$x+b,
∵点(2,3)到直线y=-2x的距离d=$\frac{7}{\sqrt{5}}$,
∴点(2,3)到直线y=$\frac{1}{2}$x+b的距离d=$\frac{|b-2|}{\sqrt{\frac{5}{4}}}$=$\frac{2|b-2|}{\sqrt{5}}$=$\frac{7}{\sqrt{5}}$,
整理得:|b-2|=$\frac{7}{2}$,即b-2=$\frac{7}{2}$或b-2=-$\frac{7}{2}$,
解得:b=$\frac{11}{2}$(不合题意,舍去)或b=-$\frac{3}{2}$,
则所求函数解析式为y=$\frac{1}{2}$x-$\frac{3}{2}$.
故答案为:y=$\frac{1}{2}$x-$\frac{3}{2}$.
点评 此题考查了一次函数综合题,涉及的知识有:待定系数法求一次函数解析式,平移、对称及旋转的性质,以及点到直线的距离公式,熟练掌握待定系数法是解本题的关键.

 名校课堂系列答案
名校课堂系列答案| A. | y=(x+3)2-2 | B. | y=(x-3)2+2 | C. | y=(x+3)2+2 | D. | y=(x-3)2-2 |
| A. | 70° | B. | 60° | C. | 50° | D. | 40° |
| A. | 10+$\frac{10}{11}$=102×$\frac{10}{11}$ | B. | 10+$\frac{10}{99}$=102×$\frac{10}{99}$ | ||
| C. | 11+$\frac{11}{12}$=112×$\frac{11}{12}$ | D. | 11+$\frac{11}{120}$=112×$\frac{11}{120}$ |

 已知线段AB=6,若O是AB的中点,点M在线段AB上,OM=1,则线段BM的长度为2或4.
已知线段AB=6,若O是AB的中点,点M在线段AB上,OM=1,则线段BM的长度为2或4.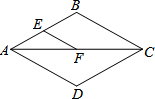 如图,AC是菱形ABCD的对角线,E、F分别是AB、AC的中点,如果EF=2,那么菱形ABCD的周长是16.
如图,AC是菱形ABCD的对角线,E、F分别是AB、AC的中点,如果EF=2,那么菱形ABCD的周长是16. 如图,在△ABC中,∠ACB=90°,D是AB中点,连接CD.若AB=10,则CD的长为( )
如图,在△ABC中,∠ACB=90°,D是AB中点,连接CD.若AB=10,则CD的长为( )