题目内容
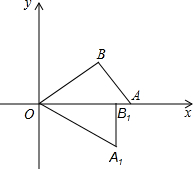 如图,O是坐标原点,∠OBA=90°,点A在x轴上,点B的坐标为(4,3),将△AOB绕点O顺时针旋转,点B的对应点B1落在x轴上,则点A的对应点A1的坐标是(________,________)
如图,O是坐标原点,∠OBA=90°,点A在x轴上,点B的坐标为(4,3),将△AOB绕点O顺时针旋转,点B的对应点B1落在x轴上,则点A的对应点A1的坐标是(________,________)
5 -
分析:要求A1坐标,须知OB1、A1B1的长度,即在△AOB中求OB、AB的长度.作BC⊥OA于点C,运用射影定理求解.
解答: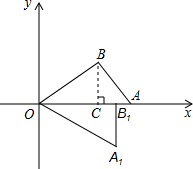 解:作BC⊥OA于点C.
解:作BC⊥OA于点C.
∵B点的坐标为(4,3),
∴OC=4,BC=3.
∴根据勾股定理得OB=5;
根据射影定理得,OB2=OC•OA,
∴OA= ,
,
∴AB= =
=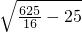 =
= =
= .
.
∴OB1=5,A1B1= .
.
∵A1在第四象限,
∴A1(5,- ).
).
故答案为:5,- .
.
点评:此题主要考查了勾股定理以及旋转的性质,此题关键是运用勾股定理和射影定理求相关线段的长度,根据点所在位置确定点的坐标.

分析:要求A1坐标,须知OB1、A1B1的长度,即在△AOB中求OB、AB的长度.作BC⊥OA于点C,运用射影定理求解.
解答:
 解:作BC⊥OA于点C.
解:作BC⊥OA于点C.∵B点的坐标为(4,3),
∴OC=4,BC=3.
∴根据勾股定理得OB=5;
根据射影定理得,OB2=OC•OA,
∴OA=
 ,
,∴AB=
 =
=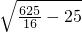 =
= =
= .
.∴OB1=5,A1B1=
 .
.∵A1在第四象限,
∴A1(5,-
 ).
).故答案为:5,-
 .
.点评:此题主要考查了勾股定理以及旋转的性质,此题关键是运用勾股定理和射影定理求相关线段的长度,根据点所在位置确定点的坐标.

练习册系列答案
相关题目
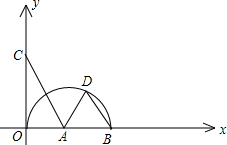 圆的直径,BD∥AC交半圆于D,其BD=2,
圆的直径,BD∥AC交半圆于D,其BD=2,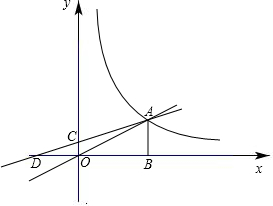 点A,过点A作AB⊥x轴,垂足为B,若OB=4,tan∠AOB=
点A,过点A作AB⊥x轴,垂足为B,若OB=4,tan∠AOB=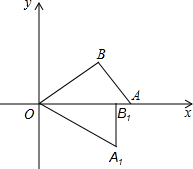 (2012•集美区一模)如图,O是坐标原点,∠OBA=90°,点A在x轴上,点B的坐标为(4,3),将△AOB绕点O顺时针旋转,点B的对应点B1落在x轴上,则点A的对应点A1的坐标是(
(2012•集美区一模)如图,O是坐标原点,∠OBA=90°,点A在x轴上,点B的坐标为(4,3),将△AOB绕点O顺时针旋转,点B的对应点B1落在x轴上,则点A的对应点A1的坐标是( (2011•犍为县模拟)如图,O是坐标原点,直线OA与双曲线
(2011•犍为县模拟)如图,O是坐标原点,直线OA与双曲线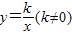 在第一象限内交于点A,过点A作AB⊥x轴,垂足为B,若OB=4,tan∠AOB=
在第一象限内交于点A,过点A作AB⊥x轴,垂足为B,若OB=4,tan∠AOB= .
.