题目内容
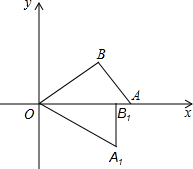 (2012•集美区一模)如图,O是坐标原点,∠OBA=90°,点A在x轴上,点B的坐标为(4,3),将△AOB绕点O顺时针旋转,点B的对应点B1落在x轴上,则点A的对应点A1的坐标是(
(2012•集美区一模)如图,O是坐标原点,∠OBA=90°,点A在x轴上,点B的坐标为(4,3),将△AOB绕点O顺时针旋转,点B的对应点B1落在x轴上,则点A的对应点A1的坐标是(5
5
,-
| 15 |
| 4 |
-
)| 15 |
| 4 |
分析:要求A1坐标,须知OB1、A1B1的长度,即在△AOB中求OB、AB的长度.作BC⊥OA于点C,运用射影定理求解.
解答: 解:作BC⊥OA于点C.
解:作BC⊥OA于点C.
∵B点的坐标为(4,3),
∴OC=4,BC=3.
∴根据勾股定理得OB=5;
根据射影定理得,OB2=OC•OA,
∴OA=
,
∴AB=
=
=
=
.
∴OB1=5,A1B1=
.
∵A1在第四象限,
∴A1(5,-
).
故答案为:5,-
.
 解:作BC⊥OA于点C.
解:作BC⊥OA于点C.∵B点的坐标为(4,3),
∴OC=4,BC=3.
∴根据勾股定理得OB=5;
根据射影定理得,OB2=OC•OA,
∴OA=
| 25 |
| 4 |
∴AB=
| AO2-OB2 |
|
|
| 15 |
| 4 |
∴OB1=5,A1B1=
| 15 |
| 4 |
∵A1在第四象限,
∴A1(5,-
| 15 |
| 4 |
故答案为:5,-
| 15 |
| 4 |
点评:此题主要考查了勾股定理以及旋转的性质,此题关键是运用勾股定理和射影定理求相关线段的长度,根据点所在位置确定点的坐标.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2012•集美区一模)如图△ABC的两条中线AD与BE相交于G,EF∥AD,EF交BC于F,已知:AG=4厘米,则DG=
(2012•集美区一模)如图△ABC的两条中线AD与BE相交于G,EF∥AD,EF交BC于F,已知:AG=4厘米,则DG=