题目内容
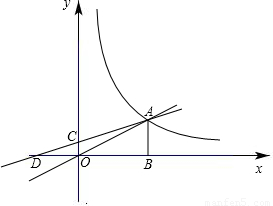
如图,O是坐标原点,A是X轴上的一点,C是Y轴上的一点,OB是以A圆心的半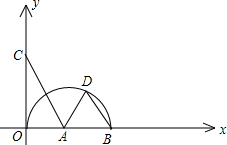 圆的直径,BD∥AC交半圆于D,其BD=2,
圆的直径,BD∥AC交半圆于D,其BD=2,(1)当A、C的坐标分别为(x,0),(0,y)时,请用x的代数式表示y;
(2)当A点的坐标为(2,0)时,求过C、D两点,顶点在直线x=2上的抛物线的解析式;
(3)在所求的抛物线上是否存在点P,使得S△POB=2S△OAD?
分析:(1)可通过构建相似三角形来求解,连接OD,那么根据A,C的坐标可得,OB=2x,OC=y,那么通过相似三角形OCA和DOB可得出关于OD,OA,BD,OB的比例关系,即可得出用x表示y的代数式.
(2)当A的坐标为2时,即x=2,然后代入(1)中各线段的表达式中,不难得出C,D两点的坐标,那么根据抛物线的顶点在x=2上,那么可用顶点式来设二次函数,然后将C,D的坐标代入即可得出抛物线的解析式.
(3)可先求出三角形POB的面积,由于OB的长为定值,因此可求出P点的纵坐标的绝对值,由于(2)的抛物线与x轴没有交点且开口向上,因此P的纵坐标为正值,然后将P点的纵坐标代入抛物线的解析式中,即可求出P点的坐标.
(2)当A的坐标为2时,即x=2,然后代入(1)中各线段的表达式中,不难得出C,D两点的坐标,那么根据抛物线的顶点在x=2上,那么可用顶点式来设二次函数,然后将C,D的坐标代入即可得出抛物线的解析式.
(3)可先求出三角形POB的面积,由于OB的长为定值,因此可求出P点的纵坐标的绝对值,由于(2)的抛物线与x轴没有交点且开口向上,因此P的纵坐标为正值,然后将P点的纵坐标代入抛物线的解析式中,即可求出P点的坐标.
解答: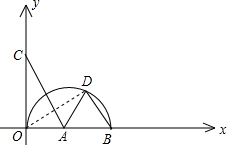 解:(1)由A(x,0),可得:B(2x,0);
解:(1)由A(x,0),可得:B(2x,0);
所以,OA=x,OB=2x,BD=2.
连接OD,则有:OD⊥BD;由勾股定理可得:OD=2
因为,BD∥AC,
所以,∠OAC=∠DBO;
而且,∠AOC=90°=∠BDO,可得:△OAC∽△DBO;
所以,
=
,
可求得:OC=x
由C(0,y),可得:y=x
.
(2)由A(2,0),利用(1)中求得的各线段表达式,
容易求得:C(0,2
),D(3,
).
设所求的顶点在直线x=2上的抛物线的解析式为y=a(x-2)2+b;
抛物线过C、D两点,将C、D两点坐标代入,
可求得:a=
,b=
.
代入抛物线的解析式,
可得:y=
x2-
x+2
.
(3)设使得S△POB=2S△OAD的点P坐标为(m,n),
则有:S△POB=2n,2S△OAD=2
;
所以,2n=2
,
解得:n=
.
点P在抛物线上,得:n=
m2-
m+2
,
将n=
代入,
可求得:m=1或m=3.
所以,存在这样的点P,其坐标为(1,
)或(3,
).
 解:(1)由A(x,0),可得:B(2x,0);
解:(1)由A(x,0),可得:B(2x,0);所以,OA=x,OB=2x,BD=2.
连接OD,则有:OD⊥BD;由勾股定理可得:OD=2
| x2-1 |
因为,BD∥AC,
所以,∠OAC=∠DBO;
而且,∠AOC=90°=∠BDO,可得:△OAC∽△DBO;
所以,
| OC |
| OD |
| OA |
| BD |
可求得:OC=x
| x2-1 |
由C(0,y),可得:y=x
| x2-1 |
(2)由A(2,0),利用(1)中求得的各线段表达式,
容易求得:C(0,2
| 3 |
| 3 |
设所求的顶点在直线x=2上的抛物线的解析式为y=a(x-2)2+b;
抛物线过C、D两点,将C、D两点坐标代入,
可求得:a=
| ||
| 3 |
2
| ||
| 3 |
代入抛物线的解析式,
可得:y=
| ||
| 3 |
4
| ||
| 3 |
| 3 |
(3)设使得S△POB=2S△OAD的点P坐标为(m,n),
则有:S△POB=2n,2S△OAD=2
| 3 |
所以,2n=2
| 3 |
解得:n=
| 3 |
点P在抛物线上,得:n=
| ||
| 3 |
4
| ||
| 3 |
| 3 |
将n=
| 3 |
可求得:m=1或m=3.
所以,存在这样的点P,其坐标为(1,
| 3 |
| 3 |
点评:本题主要考查了相似三角形的判定和性质以及二次函数的综合应用,通过构建相似三角形得出x,y的关系式是解题的关键.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
 点A,过点A作AB⊥x轴,垂足为B,若OB=4,tan∠AOB=
点A,过点A作AB⊥x轴,垂足为B,若OB=4,tan∠AOB=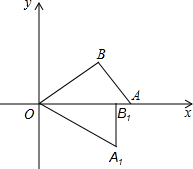 (2012•集美区一模)如图,O是坐标原点,∠OBA=90°,点A在x轴上,点B的坐标为(4,3),将△AOB绕点O顺时针旋转,点B的对应点B1落在x轴上,则点A的对应点A1的坐标是(
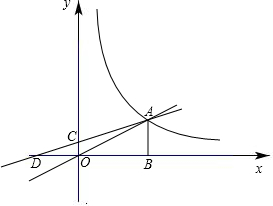
(2012•集美区一模)如图,O是坐标原点,∠OBA=90°,点A在x轴上,点B的坐标为(4,3),将△AOB绕点O顺时针旋转,点B的对应点B1落在x轴上,则点A的对应点A1的坐标是( (2011•犍为县模拟)如图,O是坐标原点,直线OA与双曲线
(2011•犍为县模拟)如图,O是坐标原点,直线OA与双曲线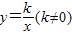 在第一象限内交于点A,过点A作AB⊥x轴,垂足为B,若OB=4,tan∠AOB=
在第一象限内交于点A,过点A作AB⊥x轴,垂足为B,若OB=4,tan∠AOB= .
.