题目内容
在一个不透明的盒子里装有黑、白两种颜色的球共40只，这些球除颜色外其余完全相同．小颖做摸球实验，搅匀后，她从盒子里随机摸出一只球记下颜色后，再把球放回盒子中，不断重复上述过程，下表是实验中的一组统计数据：
摸球的次数n | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
摸到白球的次数m | 65 | 124 | 178 | 302 | 481 | 599 | 1803 |
摸到白球的频率 | 0.65 | 0.62 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
（1）请估计：当n很大时，摸到白球的频率将会接近 ；（精确到0.1）
（2）若从盒子里随机摸出一只球，则摸到白球的概率的估计值为 ；
（3）试估算盒子里黑、白两种颜色的球各有多少只？
（1）0.6；（2）0.6；（3）盒子里黑、白两种颜色的球各有16只， 24只． 【解析】试题分析：⑴ 观察图表可知，当 很大时，摸到白球的频率接近0.6 . ⑵ 当实验次数很大时，频率接近概率，所以摸到白球的概率估值为0.6 . ⑶ 摸到白球概率为0.6，摸到黑球的概率为0.4，那么白球数量为 个， 黑球数量为 个. 试题解析：（1）∵摸到白球的频率为0.6， ...
练习册系列答案
状元及第系列答案
同步奥数系列答案
相关题目
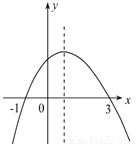
二次函数y=ax2+bx+c（a，b，c为常数，且a≠0）中的x与y的部分对应值如下表：
X | ﹣1 | 0 | 1 | 3 |
y | ﹣1 | 3 | 5 | 3 |
下列结论：
⑴ac＜0；
⑵当x＞1时，y的值随x值的增大而减小．
⑶3是方程ax2+（b﹣1）x+c=0的一个根；
⑷当﹣1＜x＜3时，ax2+（b﹣1）x+c＞0．
其中正确的个数为（ ）
A. 4个 B. 3个 C. 2个 D. 1个
B 【解析】二次函数过（-1，-1），（0,3），（1,5）， ， 解得,y=-.对称轴,, (1)正确，（2）开口向下，对称轴，x＞1时y先增大再减小,错误，（3）+2,解得， .正确，（4）+2,所以由（3）得到函数与x轴的交点，作图知，﹣1＜x＜3时,y>0正确. 所以（1）（3）（4）正确.选B.
=
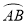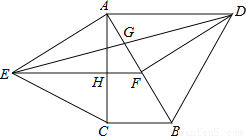
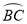，∠AOB=60°，则∠BDC的度数是（ ）.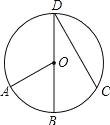
B. 
C. 
D. 
BD