题目内容
15.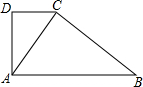 如图,ABCD是一四边形小鱼塘,边AD⊥CD,从AC分开后,变成两个相似的三角形小鱼塘,AC⊥BC,若AB,AC的长是方程x2-25x+150=0的根.
如图,ABCD是一四边形小鱼塘,边AD⊥CD,从AC分开后,变成两个相似的三角形小鱼塘,AC⊥BC,若AB,AC的长是方程x2-25x+150=0的根.(1)求CD的长;
(2)求四边形ABCD的面积.
分析 (1)先利用因式分解法解方程x2-25x+150=0得到AB=15,AC=10,接着在Rt△ACB中利用勾股定理计算出BC=5$\sqrt{5}$,分类讨论:当△ADC∽△ACB时,利用相似比可计算出CD=$\frac{10\sqrt{5}}{3}$;当△ADC∽△BCA,利用相似比可计算出CD=$\frac{50}{3}$;
(2)根据勾股定理,在Rt△ADC中,当CD=$\frac{10\sqrt{5}}{3}$,计算出AD=$\frac{50}{3}$,当CD=$\frac{50}{3}$时,计算出AD=$\frac{10\sqrt{5}}{3}$,然后根据三角形面积公式,利用四边形ABCD的面积=S△ADC+S△ABC进行计算.
解答 解:(1)∵AD⊥CD,AC⊥BC,
∴∠D=∠ACB=90°,
解方程x2-25x+150=0得x1=10,x2=15,
∴AB=15,AC=10,
在Rt△ACB中,BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=$\sqrt{1{5}^{2}-1{0}^{2}}$=5$\sqrt{5}$,
当△ADC∽△ACB时,$\frac{CD}{BC}$=$\frac{AC}{AB}$,即$\frac{CD}{5\sqrt{5}}$=$\frac{10}{15}$,解得CD=$\frac{10\sqrt{5}}{3}$,
当△ADC∽△BCA,即$\frac{CD}{CA}$=$\frac{AC}{AB}$,即$\frac{CD}{10}$=$\frac{10}{15}$,解得CD=$\frac{50}{3}$,
即CD的长为$\frac{10\sqrt{5}}{3}$或$\frac{50}{3}$;
(2)在Rt△ADC中,当CD=$\frac{10\sqrt{5}}{3}$,AD=$\sqrt{A{C}^{2}-C{D}^{2}}$=$\frac{50}{3}$,
当CD=$\frac{50}{3}$时,AD=$\sqrt{A{C}^{2}-C{D}^{2}}$=$\frac{10\sqrt{5}}{3}$,
所以四边形ABCD的面积=S△ADC+S△ABC=$\frac{1}{2}$×$\frac{50}{3}$×$\frac{10\sqrt{5}}{3}$+$\frac{1}{2}$×10×5$\sqrt{5}$=$\frac{475\sqrt{5}}{9}$.
点评 本题考查了相似三角形的应用:利用相似三角形的对应边的比相等计算线段的长.注意分类讨论思想的运用.

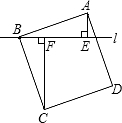 如图,过正方形ABCD的顶点B作直线l,过A、C作直线L的垂线,垂足分别为E、F,若AE=1,CF=2,则AB的长为( )
如图,过正方形ABCD的顶点B作直线l,过A、C作直线L的垂线,垂足分别为E、F,若AE=1,CF=2,则AB的长为( )| A. | $\sqrt{2}$ | B. | 2 | C. | 3 | D. | $\sqrt{5}$ |
| A. | AB=4,AD=4 | B. | AB=4,AD=7 | C. | AB=9,AD=2 | D. | AB=6,AD=2 |
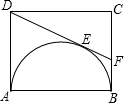 矩形ABCD中,AB=4,AD=3,以AB为直径在矩形内作半圆.DE切⊙O于点E(如图),则tan∠CDF的值为$\frac{5}{12}$.
矩形ABCD中,AB=4,AD=3,以AB为直径在矩形内作半圆.DE切⊙O于点E(如图),则tan∠CDF的值为$\frac{5}{12}$. 如图是由7×7个边长为单位1的正方形组成的大正方形,每个小正方形顶点称为格点,请连结图中的格点.
如图是由7×7个边长为单位1的正方形组成的大正方形,每个小正方形顶点称为格点,请连结图中的格点. 一个印有“我喜欢数学课”字样的立方体纸盒表面展开图如图所示,则与印有“欢”字相对的表面上印有我字.
一个印有“我喜欢数学课”字样的立方体纸盒表面展开图如图所示,则与印有“欢”字相对的表面上印有我字.