题目内容
6.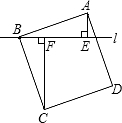 如图,过正方形ABCD的顶点B作直线l,过A、C作直线L的垂线,垂足分别为E、F,若AE=1,CF=2,则AB的长为( )
如图,过正方形ABCD的顶点B作直线l,过A、C作直线L的垂线,垂足分别为E、F,若AE=1,CF=2,则AB的长为( )| A. | $\sqrt{2}$ | B. | 2 | C. | 3 | D. | $\sqrt{5}$ |
分析 由正方形的性质得出AB=BC=CD=DA,∠ABC=90°,得出∠CBF+∠ABE=90°,证出∠BAE=∠CBF,由AAS证明△BFC≌△AEB,得出BF=AE=1,再根据勾股定理求出AB2,即可得出AB.
解答 解:∵四边形ABCD是正方形,
∴AB=BC=CD=DA,∠ABC=90°,
∴∠CBF+∠ABE=90°,
∵AE⊥l,CF⊥l,
∴∠AEB=∠CFB=90°,
∴∠ABE+∠BAE=90°,
∴∠BAE=∠CBF,
在△BFC和△AEB中,
$\left\{\begin{array}{l}{∠CFB=∠AEB}\\{∠CBF=∠BAF}\\{BC=AB}\end{array}\right.$,
∴△BFC≌△AEB(AAS),
∴BF=AE=1,CF=BE=2
∴AB2=AE2+BE2=12+22=5,
∴AB=$\sqrt{5}$,
故选D.
点评 本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,考查了直角三角形中勾股定理的运用,本题中求证△ABE≌△BCF是解题的关键.

练习册系列答案
相关题目
17.(1)已知一批商品有A、B两种型号,体积一共是20m3,质量一共是10.5吨,求A、B两种型号商品各有几件?
(2)物流公司现有可供使用的货车每辆额定载重3.5吨,容积为6m3,其收费方式有以下两种:
①按车收费:每辆车运输货物到目的地收费600元;
②按吨收费:每吨货物运输到目的地收费200元.
要将(1)中的商品一次或分批运输到目的地,宏远商贸公司应如何选择运送、付费方式运费最少?说明理由.
说明:第(2)问不必列方程.
| 体积(m3/件) | 质量(吨/件) | |
| A型商品 | 0.8 | 0.5 |
| B型商品 | 2 | 1 |
①按车收费:每辆车运输货物到目的地收费600元;
②按吨收费:每吨货物运输到目的地收费200元.
要将(1)中的商品一次或分批运输到目的地,宏远商贸公司应如何选择运送、付费方式运费最少?说明理由.
说明:第(2)问不必列方程.
14.一个多边形的边数增加2,则这个多边形的外角和( )
| A. | 增加180° | B. | 增加360° | C. | 增加540° | D. | 不变 |
18.(-16)2的算术平方根是( )
| A. | 16 | B. | 4 | C. | ±16 | D. | ±4 |
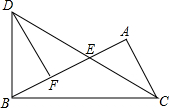 如图,在△ABC中,∠BAC=90°,过点B作BC的垂线交∠ACB的角平分线于点D,CD与AB边交于点E,过D作DF⊥AB于点F.
如图,在△ABC中,∠BAC=90°,过点B作BC的垂线交∠ACB的角平分线于点D,CD与AB边交于点E,过D作DF⊥AB于点F.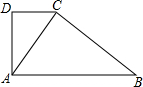 如图,ABCD是一四边形小鱼塘,边AD⊥CD,从AC分开后,变成两个相似的三角形小鱼塘,AC⊥BC,若AB,AC的长是方程x2-25x+150=0的根.
如图,ABCD是一四边形小鱼塘,边AD⊥CD,从AC分开后,变成两个相似的三角形小鱼塘,AC⊥BC,若AB,AC的长是方程x2-25x+150=0的根.