题目内容
8.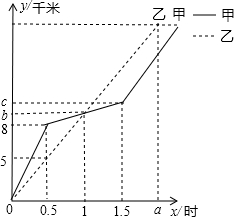 如图,表示甲、乙两人沿同一条路长跑,两人的行程y(千米)与时间x(时)变化的图象(全程)如图所示,根据图象回答问题:
如图,表示甲、乙两人沿同一条路长跑,两人的行程y(千米)与时间x(时)变化的图象(全程)如图所示,根据图象回答问题:(1)乙的速度为10千米/小时;两人是否同时到达终点不是(填“是”或“不是”);
(2)甲第一段的速度为16千米/时;第二段的速度为4千米/时;
(3)b、c表示的数字分别为10、12;
(4)若两人在相遇后1小时乙到达终点,则a表示的数字为2;甲的行程是20千米,乙的行程是20千米.
分析 (1)根据函数图象中的数据可以求得乙的速度并且判断两人是否同时到达终点;
(2)根据函数图象中的数据可以求得甲第一段和第二段的速度;
(3)根据(1)和(2)中的甲乙的速度和函数图象中的数据可以求得b和c的值;
(4)根据题意可以求得a的值,求出甲乙的行程,本题得以解决.
解答 解:(1)由题意和图象可得,
乙的速度为:5÷0.5=10千米/时,两人不是同时到达终点,
故答案为:10,不是;
(2)由图象可得,
甲第一段的速度为:8÷0.5=16千米/时,第二段的速度为:(10×1-8)÷(1-0.5)=2÷0.5=4千米/时,
故答案为:16,4;
(3)由题意可得,
b=10×1=10,c=8+(1.5-0.5)×4=8+4=12,
故答案为:10、12;
(4)由题意可得,
a=1+1=2,甲的行程是:10×2=20(千米),乙的行程与甲的一样也是20千米,
故答案为:2;20,20.
点评 本题考查一次函数的应用,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.

练习册系列答案
相关题目
16.某人先以v1的速度由A地出发去B地,途中在超市购买了一瓶水之后,又以v2的速度继续进行至B地,已知v1<v2,下面图象中能表示他从A地到B地的时间t(分钟)与路程s(千米)之间关系的是( )
| A. | 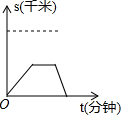 | B. | 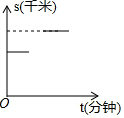 | C. | 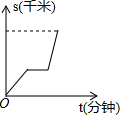 | D. |  |
20.在-1.414,$\frac{22}{7}$,$\root{3}{-27}$,$\frac{π}{3}$,-$\sqrt{2}$,3.14,$\sqrt{9}$,0.1212212221…(两个1之间依次多1个2)中,无理数的个数是( )
| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
17.下列代数式变形正确的是( )
| A. | -a+b=(a+b) | B. | -4a2+b2=(2a-b)(2a+b) | ||
| C. | (-x-y)2=(x+y)2 | D. | x2-4x-3=(x-2)2-3 |
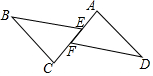 如图,点E,F在AC上,AE=CF,∠AFD=∠CEB,要使△ADF≌△CBE,需要添加的一个条件是∠A=∠C.
如图,点E,F在AC上,AE=CF,∠AFD=∠CEB,要使△ADF≌△CBE,需要添加的一个条件是∠A=∠C.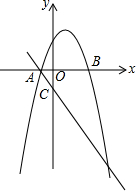 在平面直角坐标系xOy中,抛物线y=-x2+bx+c与x轴交于点A,B(A在B的左侧),抛物线的对称轴为直线x=1,AB=4.
在平面直角坐标系xOy中,抛物线y=-x2+bx+c与x轴交于点A,B(A在B的左侧),抛物线的对称轴为直线x=1,AB=4.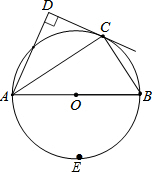 如图,在四边形ABCD中,∠D=90°,AC平分∠DAB,且点C在以AB为直径的⊙O上.
如图,在四边形ABCD中,∠D=90°,AC平分∠DAB,且点C在以AB为直径的⊙O上.