题目内容
1.设y=x2-4x+4(1)求其顶点与对称轴;
(2)求抛物线与坐标轴的交点.
分析 (1)首先把已知函数解析式配方,然后利用抛物线的顶点坐标、对称轴的公式即可求解;
(2)令y=0,求得与x轴交点坐标,令x=0,求得与y轴的交点坐标即可.
解答 解:(1)∵y=x2-4x+4=(x-2)2,
∴顶点坐标(2,0),对称轴是直线x=2;
(2)令y=0,则x2-4x+4=0,
解得x=2,
所以抛物线与x轴的交点坐标为(2,0),
令x=0,则y=4.
所以抛物线与y轴的交点坐标(0,4).
点评 此题考查二次函数的性质,掌握求对称轴、顶点坐标以及与坐标轴交点坐标的方法是解决问题的关键.

练习册系列答案
相关题目
16.某商品连续两次降价.单价由100元降至81元,若两次的降价的百分率一样,则这样百分率为( )
| A. | 10% | B. | 20% | C. | 30% | D. | 40% |
13.已知x=2是关于x的一元二次方程x2-x+2a=0的一个解,则a的值为( )
| A. | 0 | B. | -1 | C. | 1 | D. | 2 |
10.据统计,徐州旅游业今年1至10月总收入71860 000 000元,这个数用科学记数法表示为( )
| A. | 7.186×1011元 | B. | 7.186×109元 | C. | 7.186×1010元 | D. | 7.186×108元 |
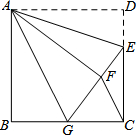 如图,在正方形ABCD中,AB=12,点E在边CD上,CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG,CF.有下列结论:①△ABG≌△AFG;②BG=GC;③AG∥CF;④S△FGC=6.其中正确的结论是①②③.
如图,在正方形ABCD中,AB=12,点E在边CD上,CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG,CF.有下列结论:①△ABG≌△AFG;②BG=GC;③AG∥CF;④S△FGC=6.其中正确的结论是①②③.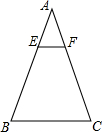 如图,在△ABC中,E、F分别是AB、AC上的点,EF∥BC,且$\frac{AE}{EB}$=$\frac{1}{2}$,若△AEF的面积为2,则四边形EBCF的面积为( )
如图,在△ABC中,E、F分别是AB、AC上的点,EF∥BC,且$\frac{AE}{EB}$=$\frac{1}{2}$,若△AEF的面积为2,则四边形EBCF的面积为( )