题目内容
 如图,⊙O的半径为4,A、B、C均是⊙O的点,点D是∠BAC的平分线与⊙O的交点,若∠BAC=120°,则弦BD的长为
如图,⊙O的半径为4,A、B、C均是⊙O的点,点D是∠BAC的平分线与⊙O的交点,若∠BAC=120°,则弦BD的长为考点:圆周角定理,勾股定理,垂径定理
专题:计算题
分析:连结BC、OB、OC,延长DO交BC与H,如图,利用角平分线定义得∠ABD=∠CAD=
∠BAC=60°,则根据圆周角定理得到∠DBC=∠BCD=60°,于是可判断△BCD为等边三角形,所以BD=BC,∠BDC=60°;再利用∠ABD=∠CAD得到弧DC=弧DB,根据垂径定理的推论得到DH⊥BC,BH=CH,接着根据圆周角定理计算出∠BOH=60°,然后在Rt△BOH中根据含30度的直角三角形三边的关系可计算出BH=2
,则BC=2BH=4
,即BD=4
.
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
解答: 解:连结BC、OB、OC,延长DO交BC与H,如图,
解:连结BC、OB、OC,延长DO交BC与H,如图,
∵AD平分∠BAC,
∴∠ABD=∠CAD=
∠BAC=60°,
∴∠DBC=∠BCD=60°,
∴△BCD为等边三角形,
∴BD=BC,∠BDC=60°,
∵∠ABD=∠CAD,
∴弧DC=弧DB,
∴DH⊥BC,
∴BH=CH,∠BOH=
∠BOC,
而∠BOC=2∠BDC=120°,
∴∠BOH=60°,
在Rt△BOH中,∵∠OBH=30°,
∴OH=
OB=2,
∴BH=
OH=2
,
∴BC=2BH=4
,
∴BD=4
.
故答案为4
.
 解:连结BC、OB、OC,延长DO交BC与H,如图,
解:连结BC、OB、OC,延长DO交BC与H,如图,∵AD平分∠BAC,
∴∠ABD=∠CAD=
| 1 |
| 2 |
∴∠DBC=∠BCD=60°,
∴△BCD为等边三角形,
∴BD=BC,∠BDC=60°,
∵∠ABD=∠CAD,
∴弧DC=弧DB,
∴DH⊥BC,
∴BH=CH,∠BOH=
| 1 |
| 2 |
而∠BOC=2∠BDC=120°,
∴∠BOH=60°,
在Rt△BOH中,∵∠OBH=30°,
∴OH=
| 1 |
| 2 |
∴BH=
| 3 |
| 3 |
∴BC=2BH=4
| 3 |
∴BD=4
| 3 |
故答案为4
| 3 |
点评:本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.也考查了垂径定理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 将一根长为6cm的木棍分成两段,每段长分别为a,b(单位:cm)且a,b都为正整数.在直角坐标系中以a,b的值,构成点A(a,b).那么点A落在抛物线y=-x2+6x-5与x轴所围成的封闭图形内部(如图,不含边界)的概率为
将一根长为6cm的木棍分成两段,每段长分别为a,b(单位:cm)且a,b都为正整数.在直角坐标系中以a,b的值,构成点A(a,b).那么点A落在抛物线y=-x2+6x-5与x轴所围成的封闭图形内部(如图,不含边界)的概率为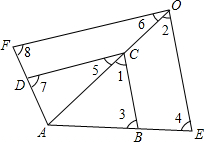 如图,已知△AEO∽△ABC,△AOF∽△ACD,那么四边形ABCD与四边形AEOF相似吗?请说明你的理由.
如图,已知△AEO∽△ABC,△AOF∽△ACD,那么四边形ABCD与四边形AEOF相似吗?请说明你的理由.