题目内容
已知抛物线y=a(x-h)2+k向左平移3个单位,再向下平移1个单位后,得到抛物线y=2(x+3)2-2
(1)求a、h、k的值;
(2)若原抛物线y=a(x-h)2+k与直线y=x+2交于B,C两点,抛物线顶点为A,求△ABC面积?
(1)求a、h、k的值;
(2)若原抛物线y=a(x-h)2+k与直线y=x+2交于B,C两点,抛物线顶点为A,求△ABC面积?
考点:二次函数图象与几何变换
专题:计算题
分析:(1)反向平移,即把抛物线y=2(x+3)2-2向右平移3个单位,再向上平移1个单位后得到抛物线y=a(x-h)2+k,然后把抛物线平移的问题转化为顶点平移的问题加以解决;
(2)先解方程组
得到B,C两点的坐标为(-1,1),(
,
),则确定顶点A的坐标为(0,-1),和直线y=x+2与y轴的交点D的坐标(0,2),然后利用△ABC=S△ABD+S△ADC进行计算.
(2)先解方程组
|
| 3 |
| 2 |
| 7 |
| 2 |
解答:解:(1)抛物线y=2(x+3)2-2的顶点坐标为(-3,-2),把点(-3,-2)向右平移3个单位,再向上平移1个单位后所得对应点的坐标为(0,-1),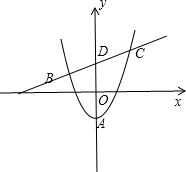
所以原抛物线的解析式为y=2x2-1,
所以a=2,b=0,k=-1;
(2)解方程组
得
或
,则B,C两点的坐标为(-1,1),(
,
)
抛物线顶点A的坐标为(0,-1),直线y=x+2与y轴的交点D的坐标为(0,2),
所以S△ABC=S△ABD+S△ADC=
×(2+1)×1+
(2+1)×
=
.

所以原抛物线的解析式为y=2x2-1,
所以a=2,b=0,k=-1;
(2)解方程组
|
|
|
| 3 |
| 2 |
| 7 |
| 2 |
抛物线顶点A的坐标为(0,-1),直线y=x+2与y轴的交点D的坐标为(0,2),
所以S△ABC=S△ABD+S△ADC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 15 |
| 4 |
点评:本题考查了二次函数图象与几何变换:由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.

练习册系列答案
相关题目
已知平面内两圆的半径分别为4和6,圆心距是4,则这两个圆的位置关系是( )
| A、相交 | B、内切 | C、外切 | D、外离 |
已知m是方程x2+x-1=0的根,则式子3m2+3m+2015的值为( )
| A、2016 | B、2017 |
| C、2018 | D、2019 |
五年前银行定期半年存款的月利率为0.75%,李明存入半年后得本息1045元,问存入银行的本金是( )
| A、1000元 |
| B、1200元 |
| C、1600元 |
| D、2000元 |
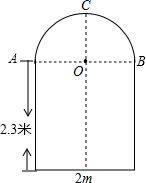 一辆装满货物的卡车,其外形高2.5米,宽1.6米,要开进厂门形状为如图所示的某工厂,厂门上部为半圆形,下部为长方形,已知长方形的宽为2米,高为2.3米,半圆形的直径与门的宽相等.问这辆卡车能否通过该工厂的厂门?
一辆装满货物的卡车,其外形高2.5米,宽1.6米,要开进厂门形状为如图所示的某工厂,厂门上部为半圆形,下部为长方形,已知长方形的宽为2米,高为2.3米,半圆形的直径与门的宽相等.问这辆卡车能否通过该工厂的厂门?