题目内容
等边△ABC中，边长AB=4，则△ABC的面积为（ ）
| A、14 | ||
| B、8 | ||
C、8
| ||
D、4
|
分析：根据等边三角形的边长可以计算等边三角形的高，根据等边三角形的边长和高即可求△ABC的面积，即可解题．
解答：
解：AD为BC边上的高，故D为BC中点，
即BD=DC=2，∵AB=4，
∴AD=
=2
，
则△ABC的面积=
BC•AD=
×4×2
=4
．
故选D．
解：AD为BC边上的高，故D为BC中点，即BD=DC=2，∵AB=4，
∴AD=
| AB2-BD2 |
| 3 |
则△ABC的面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
故选D．
点评：本题考查了三角形面积的计算，等边三角形三线合一的性质，本题中根据勾股定理求AD的值是解题的关键．
练习册系列答案
阶梯计算系列答案
相关题目
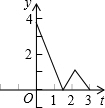
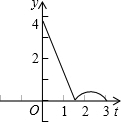
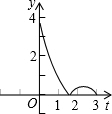
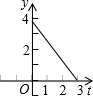
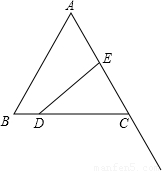
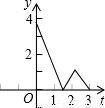
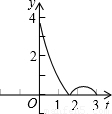
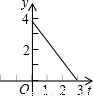
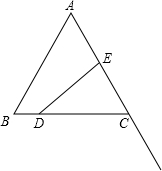（2012•延庆县二模）如图，等边△ABC中，边长AB=3，点D在线段BC上，点E在射线AC上，点D沿BC方向从B点以每秒1个单位的速度向终点C运动，点E沿AC方向从A点以每秒2个单位的速度运动，当D点停止时E点也停止运动，设运动时间为t秒，若D、E、C三点围成的图形的面积用y来表示，则y与t的图象是（ ）
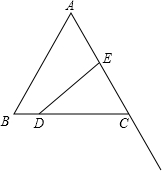如图：等边△ABC中，边长AB=3，点D在线段BC上，点E在射线AC上，点D沿BC方向从B点以每秒1个单位的速度向终点C运动，点E沿AC方向从A点以每秒2个单位的速度运动，当D点停止时E点也停止运动，设运动时间为t秒，若D、E、C三点围成的图形的面积用y来表示，则y与t的图象是
