题目内容
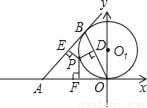
如图,OB是以(O,a)为圆心,a为半径的⊙O1的弦,过B点作⊙O1的切线,P为劣弧 上的任一点,且过P作OB、AB、OA的垂线,垂足分别是D、E、F.
上的任一点,且过P作OB、AB、OA的垂线,垂足分别是D、E、F.
(1)求证:PD2=PE•PF;
(2)当∠BOP=30°,P点为OB的中点时,求D、E、F、P四个点的坐标及S△DEF.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
甲、乙两个商场在同一周内经营同一种商品,每天的获利情况如下表:
日期 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期天 |
甲商场获利/万元 | 2.5 | 2.4 | 2.8 | 3 | 3.2 | 3.5 | 3.6 |
乙商场获利/万元 | 1.9 | 2.3 | 2.7 | 2.6 | 3 | 4 | 4.5 |
(1)请你计算出这两个商场在这周内每天获利的平均数,并说明这两个商场本周内总的获利情况;
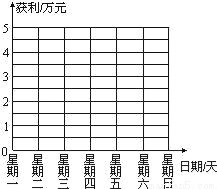
(2)在图所示的网格图内画出两个商场每天获利的折线图;(甲商场用虚线,乙商场用实线)
(3)根据折线图,请你预测下周一哪个商场的获利会多一些并简单说出你的理由.


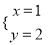 是二元一次方程组
是二元一次方程组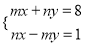 的解,则2n﹣m的平方根是_____.
的解,则2n﹣m的平方根是_____.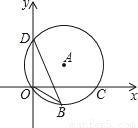
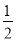 B.
B. 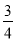 C.
C. 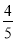 D.
D. 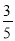
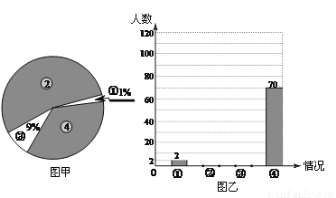
 ,则该圆锥侧面展开图的圆心角度数是___ _度.
,则该圆锥侧面展开图的圆心角度数是___ _度.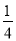 ,
, 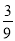 ,
, 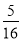 ,
, 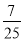 ,
, 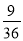 …,它们是按一定规律排列的,那么这一组数的第n个数是________.
…,它们是按一定规律排列的,那么这一组数的第n个数是________.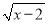 中自变量x的取值范围是( )
中自变量x的取值范围是( )