题目内容
7.已知两个全等的直角三角板ABC,DEF(如图1)放置,点B、D重合,点F在BC上,AB与EF交于点G,∠C=∠EFD=90°,∠E=∠ABC=30°,AB=DE=2.(1)求证:△EGB是等腰三角形;
(2)若△ABC不动,问△DEF绕点F顺时针最少旋转多少度时,四边形ACDE成为以DE为底的梯形?(如图2)并求此梯形的高.

分析 (1)根据题意,即可发现∠EBG=∠E=30°,从而证明结论;
(2)要使四边形ACDE成为以ED为底的梯形,则需BC⊥DE,即可求得∠BFD=30°.再根据30°的直角三角形的性质即可求解.
解答 解: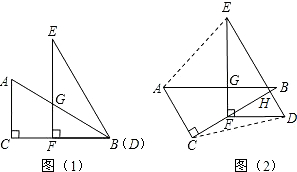 (1)证明:∵∠C=∠EFB=90°,∠E=∠ABC=30°,
(1)证明:∵∠C=∠EFB=90°,∠E=∠ABC=30°,
∴∠EBF=60°,
∴∠EBG=∠EBF-∠ABC=60°-30°=∠E.
∴GE=GB,
则△EGB是等腰三角形;
(2)解:要使四边形ACDE成为以ED为底的梯形,
则需BC⊥DE,即可求得∠BFD=30°.
∴△DEF绕点F顺时针最少旋转多少度时,四边形ACDE成为以DE为底的梯形.
设BC与DE的交点是H.
在直角三角形DFE中,∠FDH=60°,DF=$\frac{1}{2}$DE=1,
在直角三角形DFH中,FH=DF•cos∠BFD=1×cos30°=$\frac{\sqrt{3}}{2}$,
则CH=BC-BH=AB•cos∠ABC-(BF-FH)=$\sqrt{3}$-(1-$\frac{\sqrt{3}}{2}$)=$\frac{3\sqrt{3}}{2}$-2.
即此梯形的高是$\frac{3\sqrt{3}}{2}$-2.
故答案为:$\frac{3\sqrt{3}}{2}$-2.
点评 此题是三角形综合题,主要考查了含30°的直角三角形的性质,锐角三角函数,等腰三角形的判定,梯形的性质,旋转的性质,解本题的关键是求出DF.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
17.若等式$\sqrt{2}$□$\sqrt{2}$=2成立,则□内的运算符号是( )
| A. | + | B. | - | C. | × | D. | ÷ |
17.方程x2-x=2的根的判别式的值是( )
| A. | -7 | B. | 9 | C. | ±3 | D. | -9 |
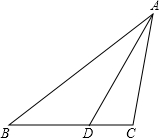 如图,在△ABC中,AC=BC,∠ACB=100°,AD是角平分线.求证:AB=AD+CD.
如图,在△ABC中,AC=BC,∠ACB=100°,AD是角平分线.求证:AB=AD+CD.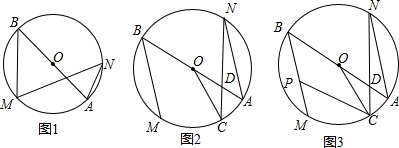
 如图,在⊙O中,∠ACB=∠D=60°,AC=3,则⊙O的直径为9.
如图,在⊙O中,∠ACB=∠D=60°,AC=3,则⊙O的直径为9.