Question

8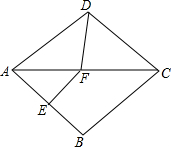．如图，菱形ABCD中，∠B=100°，AB的垂直平分线交对角线AC于点F，E为垂足，连接DF，则∠CDF等于60°．

Answer 1

分析 连接BF，根据菱形的对角线平分一组对角求出∠BAC，∠BCF=∠DCF，四条边都相等可得BC=DC，再根据菱形的邻角互补求出∠ABC，然后根据线段垂直平分线上的点到线段两端点的距离相等可得AF=BF，根据等边对等角求出∠ABF=∠BAC，从而求出∠CBF，再利用“边角边”证明△BCF和△DCF全等，根据全等三角形对应角相等可得∠CDF=∠CBF．

解答 解：如图，连接BF，
在菱形ABCD中，∵∠B=100°，
∴∠BAC=$\frac{1}{2}$∠BAD=$\frac{1}{2}$×80°=40°，∠BCF=∠DCF，BC=DC，
∵EF是线段AB的垂直平分线，
∴AF=BF，∠ABF=∠BAC=40°，
∴∠CBF=∠ABC-∠ABF=100°-40°=60°，
∵在△BCF和△DCF中，
$\left\{\begin{array}{l}{BC=DC}\\{∠BCF=∠DCF}\\{CF=CF}\end{array}\right.$，
∴△BCF≌△DCF（SAS），
∴∠CDF=∠CBF=60°，
故答案为：60．

点评 本题考查了菱形的性质，全等三角形的判定与性质，线段垂直平分线上的点到线段两端点的距离相等的性质，综合性强，但难度不大，熟记各性质是解题的关键．