题目内容
 如图,点A的坐标为(3,0),以点A为圆心,5个单位长度为半径画圆,分别交x轴于点B,C,交y轴于点E,F,求点B,C,E,F的坐标.
如图,点A的坐标为(3,0),以点A为圆心,5个单位长度为半径画圆,分别交x轴于点B,C,交y轴于点E,F,求点B,C,E,F的坐标.考点:勾股定理,坐标与图形性质
专题:
分析:由圆的半径处处相等易求C和B的坐标,连接AE,利用勾股定理可求出OE的长,进而求出点E的坐标,再根据圆的轴对称性质即可求出点F的坐标.
解答:解: 连接AE,
连接AE,
∵点A的坐标为(3,0),
∴OA=3,
∵BA=5,
∴OB=2,
∴点B的坐标是(-2,0),
∵OC=5+3=8,
∴点C的坐标是(8,0),
∵AE=5,OA=3,
∴AE=
=4,
∴点E的坐标是(0,4),
∵BC过圆心,
∴点BF的坐标是(0,-4).
 连接AE,
连接AE,∵点A的坐标为(3,0),
∴OA=3,
∵BA=5,
∴OB=2,
∴点B的坐标是(-2,0),
∵OC=5+3=8,
∴点C的坐标是(8,0),
∵AE=5,OA=3,
∴AE=
| 52-32 |
∴点E的坐标是(0,4),
∵BC过圆心,
∴点BF的坐标是(0,-4).
点评:此题考查了坐标与图形性质,以及勾股定理的运用,熟练掌握勾股定理是解本题的关键.

练习册系列答案
相关题目
若(3x+5)6=a6x6+a5x5+a4x4+a3x3+a2x2+a1x+a0,则-a6+a5-a4+a3-a2+a1-a0=( )
| A、1 | B、-1 | C、-64 | D、64 |
下列几组数中相等的是( )
| A、-8和-(-8) |
| B、23和32 |
| C、23和(-2)3 |
| D、|-a|和|a| |
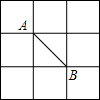 如图,A,B是3×3的正方形网格中的两个格点,C也是网格中的一个格点,连接AC、BC,当△ABC为等腰三角形时,格点C的不同位置有( )
如图,A,B是3×3的正方形网格中的两个格点,C也是网格中的一个格点,连接AC、BC,当△ABC为等腰三角形时,格点C的不同位置有( )| A、5个 | B、6个 | C、7个 | D、8个 |
抛物线y=3x2-4x+1与x轴的交点的个数为( )
| A、0 | B、1 | C、2 | D、3 |
上午8:30时,时钟的时针和分针所成的角度是( )
| A、75° | B、85° |
| C、70° | D、60° |
 将一张等宽的直角形纸片按图中的方式折叠,若∠1=36°,则∠2的度数为
将一张等宽的直角形纸片按图中的方式折叠,若∠1=36°,则∠2的度数为