题目内容
13.如图是某品牌太阳能热水器的实物图和横断面示意图,已知真空集热管AB与支架CD所在直线相交于水箱横截面⊙O的圆心,支架CD与水平面AE垂直,AB=150厘米,∠BAC=30°,另一根辅助支架DE=76厘米,∠CED=60°.则垂直支架CD的长度为38$\sqrt{3}$厘米(结果保留根号).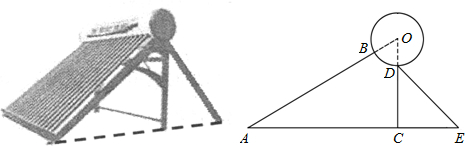
分析 由支架CD与水平面AE垂直,可得出∠DCE=90°,在Rt△DCE中由特殊角的三角函数值可求得CD的长度.
解答 解:∵支架CD与水平面AE垂直,
∴∠DCE=90°,
在Rt△DCE中,∠DCE=90°,∠CED=60°,DE=76厘米,
∴CD=DE•sin∠CED=76×sin60°=38$\sqrt{3}$(厘米).
故答案为38$\sqrt{3}$.
点评 本题考查了解直角三角形以及特殊角的三角函数值,解题的关键是熟记特殊角的三角函数值.本题属于基础题,难度不大,但题中给了干扰数据,因此再解决该类题型时,先要认真的审题,明白哪些数据有用,哪些数据无用.

练习册系列答案
相关题目
1.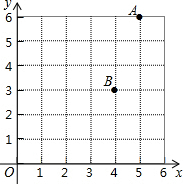 如图是某市两个小区的大致位置示意图,图中点A表示的是茗茗家所居住的小区,点B表示的是茗茗奶奶家所居住的小区,按照先列后行的顺序,点A和点B所在的位置可以表示为( )
如图是某市两个小区的大致位置示意图,图中点A表示的是茗茗家所居住的小区,点B表示的是茗茗奶奶家所居住的小区,按照先列后行的顺序,点A和点B所在的位置可以表示为( )
 如图是某市两个小区的大致位置示意图,图中点A表示的是茗茗家所居住的小区,点B表示的是茗茗奶奶家所居住的小区,按照先列后行的顺序,点A和点B所在的位置可以表示为( )
如图是某市两个小区的大致位置示意图,图中点A表示的是茗茗家所居住的小区,点B表示的是茗茗奶奶家所居住的小区,按照先列后行的顺序,点A和点B所在的位置可以表示为( )| A. | (6,5)和(3,4) | B. | (5,6)和(3,4) | C. | (6,5)和(4,3) | D. | (5,6)和(4,3) |
3.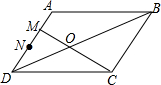 在?ABCD中,M,N是AD边上的三等分点,连接BD,MC相交于O点,则$\frac{{S}_{△MOD}}{{S}_{△COB}}$=( )
在?ABCD中,M,N是AD边上的三等分点,连接BD,MC相交于O点,则$\frac{{S}_{△MOD}}{{S}_{△COB}}$=( )
 在?ABCD中,M,N是AD边上的三等分点,连接BD,MC相交于O点,则$\frac{{S}_{△MOD}}{{S}_{△COB}}$=( )
在?ABCD中,M,N是AD边上的三等分点,连接BD,MC相交于O点,则$\frac{{S}_{△MOD}}{{S}_{△COB}}$=( )| A. | $\frac{1}{9}$或$\frac{4}{9}$ | B. | $\frac{1}{9}$ | C. | $\frac{4}{9}$ | D. | $\frac{1}{3}$或$\frac{2}{3}$ |
 如图,将平行四边形ABCD的边AB延长至点E,使AB=BE,连接BD、EC.求证:△ABD≌△BEC.
如图,将平行四边形ABCD的边AB延长至点E,使AB=BE,连接BD、EC.求证:△ABD≌△BEC.