Question

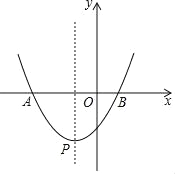
【题目】如图1，在平面直角坐标系中，直线与轴、轴分别交于点、，抛物线经过点、，且与轴的另一交点为，连接.

（1）求抛物线的解析式；

（2）点在线段上方的抛物线上，连接、，若和面积满足，求点的坐标；

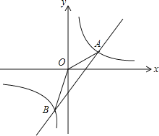
（3）如图2，为中点，设为线段上一点（不含端点），连接。一动点从出发，沿线段以每秒1个单位的速度运动到，再沿着线段以每秒个单位的速度运动到后停止。当点的坐标是多少时，点在整个运动过程中用时最少？最少时间是几秒？

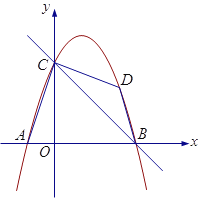
图1 图2

Answer 1

【答案】（1）；（2）或；（3）当时，最短时间为3秒，此时

【解析】

（1）根据题意得A（-1，0），B（3，0），C（0，3），用待定系数法即可求出抛物线的解析式；

（2）过D作DM∥y轴交BC于M，设，则

根据列方程求解即可；

（3）过C作CH∥x轴，过F作，根据时用时最短求解即可.

（1）当时，，

∴ ；

当时，，

∴

∵过A、B，

∴设

∵过，

∴

∴

（2）过D作DM∥y轴交BC于M

设，则

∴

∵

∴，即

∴,

∴或

（3）过C作CH∥x轴，过F作

∵在中，，∴

∵CH∥x轴，∴

∴

∴P在整个过程用的时间

∴当时，最短时间为3秒，此时