题目内容
已知：a2+2a+b2-6b+10=0，求3a+2b的值．
考点：因式分解的应用
专题：计算题
分析：先利用配方法得到（a+1）2+（b-3）2=0，再根据非负数的性质得a+1=0，b-3=0，然后解出a和b的值后代入代数式计算即可．
解答：解：∵a2+2a+b2-6b+10=0，
∴a2+2a+1+b2-6b+9=0，
∴（a+1）2+（b-3）2=0，
∴a+1=0，b-3=0，
∴a=-1，b=3，
∴3a+2b=-3+2×3=-9．
∴a2+2a+1+b2-6b+9=0，
∴（a+1）2+（b-3）2=0，
∴a+1=0，b-3=0，
∴a=-1，b=3，
∴3a+2b=-3+2×3=-9．
点评：本题考查了因式分解的应用：利用因式分解解决求值问题；利用因式分解解决证明问题；利用因式分解简化计算问题．
练习册系列答案
相关题目
如图所示，线段AB和CD的公共部分为BD，且BD=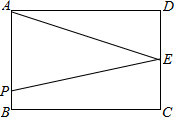
如图，长方形ABCD中，AB=4cm，BC=6cm，点E在边CD上，且DE=2，动点P从A出发，以每秒1cm的速度沿A→B→C→E运动，最终到达点E．若点P的运动时间为x秒，当x为何值时△APE的面积为7？已知二次函数y=a（x+m）2-m（a≠0），无论m为何值，图象的顶点必在（ ）
| A、直线y=-x上 | B、x轴上 |
| C、y轴上 | D、直线y=x上 |
如图，已知线段AB，在AB的延长线上取一点C，使BC=AB，在AB的反向延长线上取一点D，使DA=