题目内容
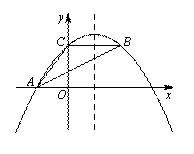
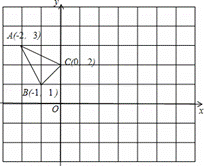
如图,抛物线y=ax2-5ax+4(a<0)经过△ABC的三个顶点,已知BC∥x轴,点A在x轴上,点C在y轴上,且AC=BC.
(1)求抛物线的解析式.
(2)在抛物线的对称轴上是否存在点M,使|MA-MB|最大?
若存在,求出点M的坐标;若不存在,请说明理由.
 |
1. 解:(1)令x=0,则y=4, ∴点C的坐标为(0,4),
∵BC∥x轴,∴点B,C关于对称轴对称,
又∵抛物线y=ax2-5ax+4的对称轴是直线 ,即直线
,即直线
∴点B的坐标为(5,4),∴AC=BC=5,
在Rt△ACO中,OA= ,∴点A的坐标为A(
,∴点A的坐标为A(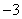 ,0),
,0),
∵抛物线y=ax2-5ax+4经过点A,∴9a+15a+4=0,解得 , ∴抛物线的解析式是
, ∴抛物线的解析式是
(2)存在,M( ,
, )
)
理由:∵B,C关于对称轴对称,∴MB=MC,∴ ;
;
∴当点M在直线AC上时, 值最大,
值最大,
设直线AC的解析式为 ,则
,则 ,解得
,解得 ,∴
,∴
令 ,则
,则 ,∴M(
,∴M( ,
, )
)

练习册系列答案
相关题目

 ,配方后的方程是
,配方后的方程是 B.
B. C.
C. D.
D.
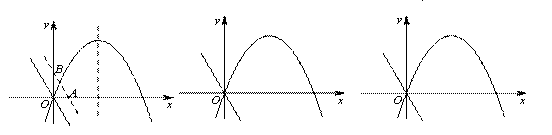
 x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).
x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).


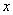 的不等式组
的不等式组 只有3个整数解,则实数
只有3个整数解,则实数 的取值范围是 .
的取值范围是 .