题目内容
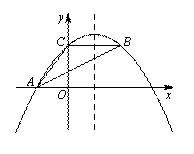
如图,抛物线y= x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).
x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).


(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)点M是x轴上的一个动点,当△DCM的周长最小时,求点M的坐标.
解:(1)∵点 在抛物线
在抛物线 上,
上,
∴ ,∴
,∴ ,
,
∴抛物线的解析式为 .
.
∵ ,
,
∴顶点D的坐标为 .
.
(2)△ABC是直角三角形.当 时,
时, ,∴
,∴ ,则
,则 .
.
当 时,
时, ,∴
,∴ ,则
,则 .
.
∴ ,
, , ∴
, ∴ .
.
∵ ,
, ,
, ,
,
∴ ,
,
∴△ABC是直角三角形.
(3)作出点C关于 轴的对称点C′,则
轴的对称点C′,则 .
.
连接C′D交 轴于点M,根据轴对称性及两点之间线段最短可知,CD一定,当MC+MD的值最小时,△CDM的周长最小.
轴于点M,根据轴对称性及两点之间线段最短可知,CD一定,当MC+MD的值最小时,△CDM的周长最小.


设直线C′D的解析式为 ,则:
,则:
则 ,解得
,解得 ,
,
∴ 当
当 时,
时, ,则
,则 ,
,
∴ .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 的两根分别为
的两根分别为 和
和 ,则
,则 的值是_____________.
的值是_____________. .
.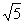 个单位长度的速度沿射线DA向上平移,直至正方形的顶点C落在y轴上时停止运动.在运动过程中,设正方形落在y轴右侧部分的面积为S,求S关于平移时间t(秒)的函数关系式,并写出相应的自变量t的取值范围.
个单位长度的速度沿射线DA向上平移,直至正方形的顶点C落在y轴上时停止运动.在运动过程中,设正方形落在y轴右侧部分的面积为S,求S关于平移时间t(秒)的函数关系式,并写出相应的自变量t的取值范围.
 <-
<- C、4a-3>4b-3 D、(c-1)2a>(c-1)2b
C、4a-3>4b-3 D、(c-1)2a>(c-1)2b 的结果是( )
的结果是( ) (B)
(B) (C)
(C) (D)
(D)