题目内容
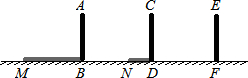
1.如图,在一个坡度i=1:7的斜坡面BD上,架设两根高度均为10米的电杆DC和BA,水平距离DE为14米,电线在空中架设时,A、C两端挂起的电线下垂近似成抛物线y=$\frac{1}{98}$x2形状,在竖直方向上,求下垂电线与坡面的距离MF的最小值.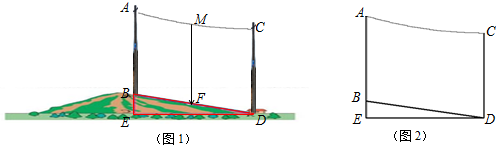
分析 以点A为原点,建立坐标系,由在一个坡度i=1:7的斜坡面BD上,水平距离DE为14米,求得BE=2m,设A点坐标为原点,根据架设两根高度均为10米的电杆DC和BA,求得C(14,-2),设此抛物线解析式为:y=$\frac{1}{98}$x2+bx,把C(14,-2)代入-2=$\frac{1}{98}$×142+b×14,解得b=-$\frac{2}{7}$,于是得到y=$\frac{1}{98}$x2-$\frac{2}{7}$x=$\frac{1}{98}$(x2-28x)=$\frac{1}{98}$(x-14)2-2,设抛物线的顶点为M,则M(14,-2),由C(14,-2),求得M与C重合,过C作CH⊥BD于H,得到△CDH∽△DBE,根据相似三角形的性质即可得到结论.
解答 解:如图,以点A为原点,建立坐标系,
∵在一个坡度i=1:7的斜坡面BD上,水平距离DE为14米,
∴BE:DE=1:7,
∴BE=2m,
设A点坐标为原点,
∵架设两根高度均为10米的电杆DC和BA,
∴C(14,-2),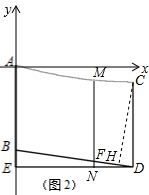
∵A、C两端挂起的电线下垂近似成抛物线y=$\frac{1}{98}$x2形状,
∴设此抛物线解析式为:y=$\frac{1}{98}$x2+bx,
-2=$\frac{1}{98}$×142+b×14,
解得:b=-$\frac{2}{7}$,
∴y=$\frac{1}{98}$x2-$\frac{2}{7}$x=$\frac{1}{98}$(x2-28x)=$\frac{1}{98}$(x-14)2-2,
∴设抛物线的顶点为M,则M(14,-2),∵C(14,-2),
∴M与C重合,
过C作CH⊥BD于H,∴△CDH∽△DBE,
∴$\frac{CH}{DE}=\frac{CD}{DB}$,
∵DB=$\sqrt{{2}^{2}+1{4}^{2}}$=10$\sqrt{2}$,
∴CH=7$\sqrt{2}$,
∴下垂电线与坡面的距离MF的最小值是7$\sqrt{2}$m.
点评 本题主要考查了二次函数在实际生活中的应用,相似三角形的判定和性质,勾股定理,熟练运用二次函数的性质是解题的关键.

 导学全程练创优训练系列答案
导学全程练创优训练系列答案 ,其中
,其中 .
. 的方程组
的方程组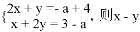 的值为( )
的值为( ) C. 0 D. 1
C. 0 D. 1
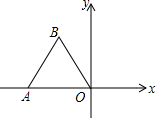 如图,△OAB是边长为2的等边三角形.
如图,△OAB是边长为2的等边三角形.