题目内容
已知,P、Q是△ABC的边BC上的两点,且BP=PC=AC,PQ=QC.
(1)如图1,当AP=AC时,求∠BAP和∠PAQ的度数.
(2)如图2,当AP≠AC时,猜想并验证∠BAP和∠PAQ的数量关系.
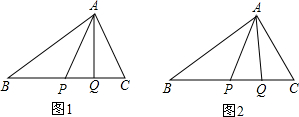
(1)如图1,当AP=AC时,求∠BAP和∠PAQ的度数.
(2)如图2,当AP≠AC时,猜想并验证∠BAP和∠PAQ的数量关系.
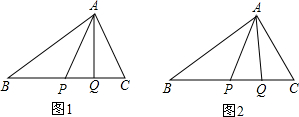
考点:等腰三角形的性质,三角形内角和定理,三角形的外角性质
专题:
分析:(1)先由△APC是等边三角形,得出∠APC=∠PAC=60°,再由等腰三角形的性质及三角形外角的性质得出∠BAP=30°,根据等腰三角形三线合一的性质得出∠PAQ=
∠PAC=30°,于是∠BAP=∠PAQ;
(2)取AC中点M,连接PM,QM.在△CAB中,根据三角形中位线的性质得出PM∥AB,PM=
AB,那么∠BAP=∠APM,再证明△APQ≌△PAM,得出∠PAQ=∠APM,于是∠BAP=∠PAQ.
| 1 |
| 2 |
(2)取AC中点M,连接PM,QM.在△CAB中,根据三角形中位线的性质得出PM∥AB,PM=
| 1 |
| 2 |
解答:解:(1)∵AP=AC,PC=AC,
∴△APC是等边三角形,
∴∠APC=∠PAC=60°,
∵BP=AP,
∴∠BAP=∠B,
∵∠BAP+∠B=∠APC=60°,
∴∠BAP=30°,
∵AP=AC,PQ=QC,
∴∠PAQ=
∠PAC=30°,
∴∠BAP=∠PAQ;
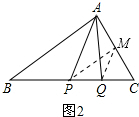 (2)取AC中点M,连接PM,QM.
(2)取AC中点M,连接PM,QM.
△CAB中,∵BP=PC,AM=MC,
∴PM∥AB,PM=
AB,
∴∠BAP=∠APM,
∵PC=AC,
∴∠APQ=∠PAM,
∵PQ=QC=
PC,AM=MC=
AC,
∴PQ=AM,
在△APQ和△PAM中,
,
∴△APQ≌△PAM(SAS),
∴∠PAQ=∠APM,
∴∠BAP=∠PAQ.
∴△APC是等边三角形,
∴∠APC=∠PAC=60°,
∵BP=AP,
∴∠BAP=∠B,
∵∠BAP+∠B=∠APC=60°,
∴∠BAP=30°,
∵AP=AC,PQ=QC,
∴∠PAQ=
| 1 |
| 2 |
∴∠BAP=∠PAQ;
 (2)取AC中点M,连接PM,QM.
(2)取AC中点M,连接PM,QM.△CAB中,∵BP=PC,AM=MC,
∴PM∥AB,PM=
| 1 |
| 2 |
∴∠BAP=∠APM,
∵PC=AC,
∴∠APQ=∠PAM,
∵PQ=QC=
| 1 |
| 2 |
| 1 |
| 2 |
∴PQ=AM,
在△APQ和△PAM中,
|
∴△APQ≌△PAM(SAS),
∴∠PAQ=∠APM,
∴∠BAP=∠PAQ.
点评:本题考查了等腰三角形的性质,三角形外角的性质,等边三角形、全等三角形的判定与性质,有一定难度.准确作出辅助线是解决第(2)小题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在6,-3,0,-2这四个数中,最小的数是( )
| A、6 | B、-3 | C、0 | D、-2 |
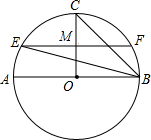 如图所示,AB是⊙O的直径,C点在⊙O上,过C作CO⊥AB,过OC的中点M作弦EF∥AB,连接BE,BC,求EF与AB的比值.
如图所示,AB是⊙O的直径,C点在⊙O上,过C作CO⊥AB,过OC的中点M作弦EF∥AB,连接BE,BC,求EF与AB的比值.