题目内容
不论x、y为何值，代数式x2+4y2+6x-4y+11的最小值是 ．
考点：配方法的应用,非负数的性质：偶次方
专题：
分析：把代数式x2+4y2+6x-4y+11根据完全平方公式化成几个完全平方和的形式，再进行求解．
解答：解：∵x2+4y2+6x-4y+11=（x+3）2+（2y+1）2+1，
故不论x、y为何实数，代数式x2+4y2+6x-4y+11的最小值是1．
故答案为：1．
故不论x、y为何实数，代数式x2+4y2+6x-4y+11的最小值是1．
故答案为：1．
点评：本题考查了完全平方公式及非负数的性质，属于基础题，关键是把代数式化成几个完全平方和的形式．
练习册系列答案
相关题目
已知，P、Q是△ABC的边BC上的两点，且BP=PC=AC，PQ=QC．
（1）如图1，当AP=AC时，求∠BAP和∠PAQ的度数．
（2）如图2，当AP≠AC时，猜想并验证∠BAP和∠PAQ的数量关系．
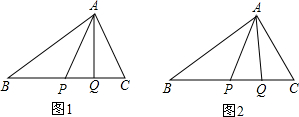
（1）如图1，当AP=AC时，求∠BAP和∠PAQ的度数．
（2）如图2，当AP≠AC时，猜想并验证∠BAP和∠PAQ的数量关系．
如图，△ABC与△A′B′C′关于直线l成轴对称，已知∠A=50°，∠C′=30°，则∠B=
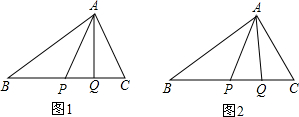
如图，△ABC≌△BAD，AC与BD是对应边，AC=8cm，AD=10cm，DE=CE=2cm，那么AE的长是下列说法中正确的是（ ）
A、
| ||
B、
| ||
| C、-5x2的系数是5 | ||
| D、3x2y的次数是2 |
下列说法中，正确的是（ ）
| A、有最小的有理数 |
| B、有最小的负数 |
| C、有绝对值最小的数 |
| D、有最小的正数 |