题目内容
 如图,E为Rt△ABC斜边上一点,四边形BFED为正方形,若BC=6,AB=8,则正方形BFED的边长为
如图,E为Rt△ABC斜边上一点,四边形BFED为正方形,若BC=6,AB=8,则正方形BFED的边长为
- A.
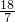
- B.

- C.4
- D.3
B
分析:正方形各边长相等,故DE=EF=BD=BF,根据DE与BC的比值和EF与AB的比值即可求得BD的值,即可解题.
解答:∵正方形BDEF
∴DE=EF=BD=BF,∵DE∥BC,EF∥AB,
∴△ADE∽△ABC,△CFE∽△CBA,
∴ =
= ,
, =
= ,AE+EC=AC
,AE+EC=AC
∴ +
+ =
= =1,
=1,
解得DE= .
.
故选B.
点评:本题考查了平行线定理,考查了相似三角形对应边比值相等的性质,考查了相似三角形的判定,本题中求证 =
= ,
, =
= 是解题的关键.
是解题的关键.
分析:正方形各边长相等,故DE=EF=BD=BF,根据DE与BC的比值和EF与AB的比值即可求得BD的值,即可解题.
解答:∵正方形BDEF
∴DE=EF=BD=BF,∵DE∥BC,EF∥AB,
∴△ADE∽△ABC,△CFE∽△CBA,
∴
 =
= ,
, =
= ,AE+EC=AC
,AE+EC=AC∴
 +
+ =
= =1,
=1,解得DE=
 .
.故选B.
点评:本题考查了平行线定理,考查了相似三角形对应边比值相等的性质,考查了相似三角形的判定,本题中求证
 =
= ,
, =
= 是解题的关键.
是解题的关键. 
练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目
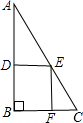 如图,E为Rt△ABC斜边上一点,四边形BFED为正方形,若BC=6,AB=8,则正方形BFED的边长为( )
如图,E为Rt△ABC斜边上一点,四边形BFED为正方形,若BC=6,AB=8,则正方形BFED的边长为( )A、
| ||
B、
| ||
| C、4 | ||
| D、3 |
 6、如图,CD为Rt△ABC斜边上的高,∠BAC的平分线分别交CD、CB于点E、F,FG⊥AB,垂足为G,则CF
6、如图,CD为Rt△ABC斜边上的高,∠BAC的平分线分别交CD、CB于点E、F,FG⊥AB,垂足为G,则CF 15、如图,D为Rt△ABC中斜边BC上的一点,且BD=AB,过D作BC的垂线,交AC于E,若AE=12cm,则DE的长为
15、如图,D为Rt△ABC中斜边BC上的一点,且BD=AB,过D作BC的垂线,交AC于E,若AE=12cm,则DE的长为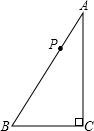 如图,P为Rt△ABC斜边AB上任意一点(除A、B外),过点P作直线截△ABC,使截得的新三角形与△ABC相似,满足这样条件的直线的作法共有
如图,P为Rt△ABC斜边AB上任意一点(除A、B外),过点P作直线截△ABC,使截得的新三角形与△ABC相似,满足这样条件的直线的作法共有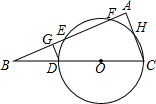 如图,D为Rt△ABC斜边BC上的一点,以CD为直径作⊙O交边AB于E、F两点,交AC于H,DG⊥AB于点G
如图,D为Rt△ABC斜边BC上的一点,以CD为直径作⊙O交边AB于E、F两点,交AC于H,DG⊥AB于点G