题目内容
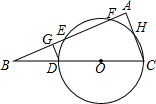 如图,D为Rt△ABC斜边BC上的一点,以CD为直径作⊙O交边AB于E、F两点,交AC于H,DG⊥AB于点G
如图,D为Rt△ABC斜边BC上的一点,以CD为直径作⊙O交边AB于E、F两点,交AC于H,DG⊥AB于点G (1)求证:AF=GE;
(2)若AF=2,FG=AC=4,求⊙O的半径.
分析:(1)连接DH、CI,过点O作OM⊥AG,垂足为点M,EM=FM,再证出GD∥AC∥OM,根据OD=OC,得出GM=AM,即可证出AF=GE,
(2)先证出四边形AGDH是矩形,求出AG、EF,得出DH=AG=6,再根据AF•AE=AH•AC求出AH=2,得出CH=2,最后根据勾股定理得出CD2=40,CD=2
,最后根据圆O的半径=
CD即可得出答案.
(2)先证出四边形AGDH是矩形,求出AG、EF,得出DH=AG=6,再根据AF•AE=AH•AC求出AH=2,得出CH=2,最后根据勾股定理得出CD2=40,CD=2
| 10 |
| 1 |
| 2 |
解答:解:(1)连接DH,过点O作OM⊥AG,垂足为点M,
则EM=FM,
∵CD为直径,
∴∠DHC=90,
∵DG⊥AB,△ABC是直角三角形,
∴GD∥AC∥OM,
∵OD=OC,
∴GM=AM,
∴GM-EM=AM-FM,
∴AF=GE;
(2)∵GD∥AC,∠DHC=90,DG⊥AB,△ABC是直角三角形,
∴四边形AGDH是矩形,
∵AG=AF+FG=2+4=6,EF=FG-GE=FG-AF=4-2=2,
∴DH=AG=6,
∵AF•AE=AH•AC,
∴2×4=AH×4
∴AH=2,
∴CH=2,
∴CD2=DH2+CH2=62+22=40,
∴CD=2
,
∴圆O的半径=
CD=
×2
=
.
则EM=FM,
∵CD为直径,
∴∠DHC=90,

∵DG⊥AB,△ABC是直角三角形,
∴GD∥AC∥OM,
∵OD=OC,
∴GM=AM,
∴GM-EM=AM-FM,
∴AF=GE;
(2)∵GD∥AC,∠DHC=90,DG⊥AB,△ABC是直角三角形,
∴四边形AGDH是矩形,
∵AG=AF+FG=2+4=6,EF=FG-GE=FG-AF=4-2=2,
∴DH=AG=6,
∵AF•AE=AH•AC,
∴2×4=AH×4
∴AH=2,
∴CH=2,
∴CD2=DH2+CH2=62+22=40,
∴CD=2
| 10 |
∴圆O的半径=
| 1 |
| 2 |
| 1 |
| 2 |
| 10 |
| 10 |
点评:此题考查了圆的综合,用到的知识点是垂经定理、勾股定理、割线定理、矩形的性质与判定,关键是综合运用有关性质,作出辅助线,列出算式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
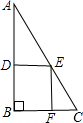 如图,E为Rt△ABC斜边上一点,四边形BFED为正方形,若BC=6,AB=8,则正方形BFED的边长为( )
如图,E为Rt△ABC斜边上一点,四边形BFED为正方形,若BC=6,AB=8,则正方形BFED的边长为( )A、
| ||
B、
| ||
| C、4 | ||
| D、3 |
 6、如图,CD为Rt△ABC斜边上的高,∠BAC的平分线分别交CD、CB于点E、F,FG⊥AB,垂足为G,则CF
6、如图,CD为Rt△ABC斜边上的高,∠BAC的平分线分别交CD、CB于点E、F,FG⊥AB,垂足为G,则CF 15、如图,D为Rt△ABC中斜边BC上的一点,且BD=AB,过D作BC的垂线,交AC于E,若AE=12cm,则DE的长为
15、如图,D为Rt△ABC中斜边BC上的一点,且BD=AB,过D作BC的垂线,交AC于E,若AE=12cm,则DE的长为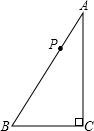 如图,P为Rt△ABC斜边AB上任意一点(除A、B外),过点P作直线截△ABC,使截得的新三角形与△ABC相似,满足这样条件的直线的作法共有
如图,P为Rt△ABC斜边AB上任意一点(除A、B外),过点P作直线截△ABC,使截得的新三角形与△ABC相似,满足这样条件的直线的作法共有