题目内容
(1)已知方程组 ,由于甲看错了方程①中的a得到方程组的解为
,由于甲看错了方程①中的a得到方程组的解为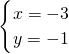 ;乙看错了方程②中的b得到方程组的解为
;乙看错了方程②中的b得到方程组的解为 ,若按正确的a、b计算,则原方程组的解为______.
,若按正确的a、b计算,则原方程组的解为______.
(2)若3a2n+m和4an-2m都是2a5的同类项,则 的值是______.
的值是______.
解:(1)把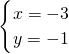 代入方程②得-12+b=-2,
代入方程②得-12+b=-2,
解得b=10;
把 代入此方程组①得5a+20=15,
代入此方程组①得5a+20=15,
解得a=-1,
把 代入原方程组得
代入原方程组得 ,
,
解得 ;
;
故答案为 ;
;
(2)根据同类项的定义可得, ,
,
解得 ,
,
 ,
,
=2n6m10× ×nm3,
×nm3,
=4n2m12,
=4×32×(-1)12,
=36.
分析:(1)先把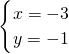 代入方程组中的方程②得到关于b的方程,求出b的值,再把
代入方程组中的方程②得到关于b的方程,求出b的值,再把 代入此方程组①求出a的值,即可得到原方程组,解此方程组即可;
代入此方程组①求出a的值,即可得到原方程组,解此方程组即可;
(2)先根据同类项的定义列出关于m、n的二元一次方程组,求出m、n的值,再把所求代数式化简,把m、n的值代入求解即可.
点评:本题考查的是解二元一次方程组及同类项的定义,即所含字母相同,并且相同字母的指数也相同,这样的项叫做同类项.
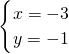 代入方程②得-12+b=-2,
代入方程②得-12+b=-2,解得b=10;
把
 代入此方程组①得5a+20=15,
代入此方程组①得5a+20=15,解得a=-1,
把
 代入原方程组得
代入原方程组得 ,
,解得
 ;
;故答案为
 ;
;(2)根据同类项的定义可得,
 ,
,解得
 ,
, ,
,=2n6m10×
 ×nm3,
×nm3,=4n2m12,
=4×32×(-1)12,
=36.
分析:(1)先把
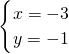 代入方程组中的方程②得到关于b的方程,求出b的值,再把
代入方程组中的方程②得到关于b的方程,求出b的值,再把 代入此方程组①求出a的值,即可得到原方程组,解此方程组即可;
代入此方程组①求出a的值,即可得到原方程组,解此方程组即可;(2)先根据同类项的定义列出关于m、n的二元一次方程组,求出m、n的值,再把所求代数式化简,把m、n的值代入求解即可.
点评:本题考查的是解二元一次方程组及同类项的定义,即所含字母相同,并且相同字母的指数也相同,这样的项叫做同类项.

练习册系列答案
相关题目
已知P(1,-2)是反比例函数y=
与正比例函数y=ax图象的一个交点,那么,由y=
与y=ax组成的方程组的解为( )
| k |
| x |
| k |
| x |
A、
| ||||||||||
B、
| ||||||||||
C、
| ||||||||||
D、
|