题目内容
8.化简代数式$\frac{{x}^{2}-1}{{x}^{2}+2x}$÷$\frac{x-1}{x}$,并判断当x满足不等式$\left\{\begin{array}{l}{-x<1}\\{2(x-1)>-6}\end{array}\right.$时该代数式的符号.分析 原式利用除法法则变形,约分得到最简结果,求出不等式组的解集即可找出判断.
解答 解:原式=$\frac{(x+1)(x-1)}{x(x+2)}$•$\frac{x}{x-1}$=$\frac{x+1}{x+2}$,
不等式组$\left\{\begin{array}{l}{-x<1①}\\{2(x-1)>-6②}\end{array}\right.$,
由①得:x>-1,
由②得:x>-2,
则不等式的解集为x>-1,
∴x+1>0,x+2>0,
则该代数式的符合为正.
点评 此题考查了分式的化简求值,以及解一元一次不等式组,熟练掌握运算法则是解本题的关键.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
19.某班去看演出,甲种票每张23元,乙种票每张18元.如果35名学生购票恰好用去730元,则( )
| A. | 甲种票买了10张,乙种票买了25张 | B. | 甲种票买了15张,乙种票买了20张 | ||
| C. | 甲种票买了20张,乙种票买了15张 | D. | 甲种票买了25张,乙种票买了10张 |
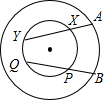 如图,在以O为圆心的两个同心圆中,A,B是大圆上任意两点,过A,B作小圆的割线AXY和BPQ.求证:AX•AY=BP•BQ.
如图,在以O为圆心的两个同心圆中,A,B是大圆上任意两点,过A,B作小圆的割线AXY和BPQ.求证:AX•AY=BP•BQ.