Question

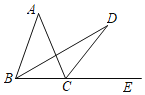
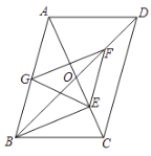
【题目】如图，中，对角线，相交于，，、、分别是、、的中点，下列结论：①；②四动形是平行四边形；③；④平分.其中正确的是（ ）

A. ①②③B. ①②④C. ①③④D. ②③④

Answer 1

【答案】B

【解析】

由平行四边形的性质可得OB=BC，由等腰三角形的性质可判断①正确，由直角三角形的性质和三角形中位线定理可判断③错误，由BG=EF，BG∥EF∥CD可证四边形BEFG是平行四边形，可得②正确．由平行线的性质和等腰三角形的性质可判断④正确．

解：如图，

∵四边形ABCD是平行四边形

∴BO=DO=BD，AD=BC，AB=CD，

又∵BD=2AD，

∴OB=BC=OD=DA，且点E 是OC中点，

∴BE⊥AC，

故①正确，

∵E、F分别是OC、OD的中点，

∴EF∥CD，EF=CD，

∵点G是Rt△ABE斜边AB上的中点，

∴GE=AB=AG=BG

∴EG=EF=AG=BG，无法证明GE=GF，

故③错误，

∵BG=EF，BG∥EF∥CD

∴四边形BEFG是平行四边形

故②正确，

∵EF∥CD∥AB，

∴∠BAC=∠ACD=∠AEF，

∵AG=GE，

∴∠GAE=∠AEG，

∴∠AEG=∠AEF，

∴AE平分∠GEF，故④正确；

故选：B．