题目内容
如图，在四边形ABCD中，E、F分别是AB、AD的中点，若EF＝6，BC＝13，CD＝5，则tan C等于 ▲ ．
 | |||
 | |||
分析：根据中位线的性质得出EF∥BD，且等于 
BD，进而得出△BDC是直角三角形，求出即可．
解：
连接BD，
∵E、F分别是AB、AD的中点，
∴EF∥BD，且等于BD，
∴BD=12，
∵BD=12，BC=13，CD=5，
∴△BDC是直角三角形，
∴tan C=
=
．
故答案为：．
BD，进而得出△BDC是直角三角形，求出即可．解：
连接BD，
∵E、F分别是AB、AD的中点，
∴EF∥BD，且等于
BD，∴BD=12，
∵BD=12，BC=13，CD=5，
∴△BDC是直角三角形，
∴tan C=
=．故答案为：
．
练习册系列答案
相关题目
，
的一个实数根。
ABC中，∠B = 45°，∠C = 60°，AB = 6。求BC的长（结果保留根号）。
上建有一座电信信号发射架
，现在山脚
处测得峰顶的仰角为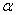
，发射架顶端的仰角为
，其中
，求发射架高
，那么AB的长为（ ▲ ）
米；
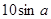米；
米；
米．