题目内容
 如图,△ABC内接于⊙O,弦CD=BC,弦AC与BD相交于点P,证明:△CAB∽△CBP.
如图,△ABC内接于⊙O,弦CD=BC,弦AC与BD相交于点P,证明:△CAB∽△CBP.考点:相似三角形的判定,圆周角定理
专题:证明题
分析:根据等腰三角形的性质由CD=BC得∠CBD=∠D,再根据圆周角定理由∠D=∠A,所以∠CBD=∠A,加上公共角,于是可根据有两组角对应相等的两个三角形相似判断△CAB∽△CBP.
解答:证明:∵CD=BC,
∴∠CBD=∠D,
∵∠D=∠A,
∴∠CBD=∠A,
∵∠BCP=∠ACB,
∴△CAB∽△CBP.
∴∠CBD=∠D,
∵∠D=∠A,
∴∠CBD=∠A,
∵∠BCP=∠ACB,
∴△CAB∽△CBP.
点评:本题考查了三角形相似的判定:有两组角对应相等的两个三角形相似.也考查了圆周角定理.

练习册系列答案
相关题目
2013年1-7月广州市财政收入增势稳定,完成地方公共财政预算收入653.6亿,将653.6亿元用科学记数法表示正确的是( )
| A、6.536×102亿元 |
| B、6.536×103亿元 |
| C、0.6536×103 |
| D、65.36×10亿元 |
下列说法中正确的是( )
| A、延长射线OA到点B |
| B、线段AB为直线AB的一部分 |
| C、射线OM与射线MO表示同一条射线 |
| D、一条直线由两条射线组成 |
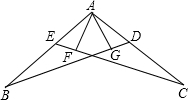 如图,AB=AC,AG⊥BD,AF⊥CE,AG=AF,求证:AD=AE.
如图,AB=AC,AG⊥BD,AF⊥CE,AG=AF,求证:AD=AE.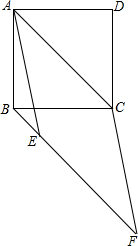 如图,已知AC是正方形ABCD的对角线,BE∥AC,点E在BF上,且AE=AC,CF∥AE,求∠BCF.
如图,已知AC是正方形ABCD的对角线,BE∥AC,点E在BF上,且AE=AC,CF∥AE,求∠BCF. 如图,已知△ABC.
如图,已知△ABC.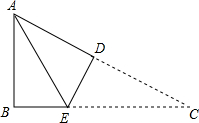 如图,在△ABC中,∠B=90°,∠C=30°,AB=3,BC=3
如图,在△ABC中,∠B=90°,∠C=30°,AB=3,BC=3