Question

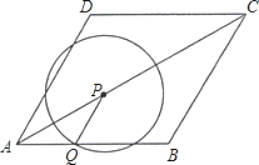
【题目】如图，菱形ABCD的边长为2cm，∠DAB＝60°．点P从A点出发，以cm/s的速度，沿AC向C作匀速运动；与此同时，点Q也从A点出发，以1cm/s的速度，沿射线AB作匀速运动．当P运动到C点时，P、Q都停止运动，设点P运动的时间为t（s）．

（1）对角线AC的长是 cm；

（2）当P异于A、C时，请说明PQ∥BC；

（3）以P为圆心、PQ长为半径作圆，请问：在整个运动过程中，t为怎样的值时，⊙P与边BC分别有1个公共点和2个公共点？

Answer 1

【答案】（1）2$\sqrt{3}$；（2）见解析；（3）当t＝4﹣6或1＜t≤3﹣或t＝2时，⊙P与菱形ABCD的边BC有1个公共点；当4﹣6＜t≤1时，⊙P与边BC有2个公共点

【解析】

（1）连接BD交AC于点O，由菱形的性质可知△AOB为直角三角形且∠OAB=30°，依据特殊锐角三角函数值可求得AO的长，从而得到AC的长；
（2）连接BD交AC于O，构建直角三角形AOB．利用菱形的对角线互相垂直、对角线平分对角、邻边相等的性质推知△PAQ∽△CAB；然后根据“相似三角形的对应角相等”证得∠APQ=∠ACB；最后根据平行线的判定定理“同位角相等，两直线平行”可以证得结论；
（3）如图2，⊙P与BC切于点M，连接PM，构建Rt△CPM，在Rt△CPM利用特殊角的三角函数值求得PM=PC=，然后根据PM=PQ=AQ=t列出关于t的方程，通过解方程即可求得t的值；
如图3，⊙P过点B，此时PQ=PB，根据等边三角形的判定可以推知△PQB为等边三角形，然后由等边三角形的性质以及（2）中求得t的值来确定此时t的取值范围；
如图4，⊙P过点C，此时PC=PQ，据此等量关系列出关于t的方程，通过解方程求得t的值．

（1）连接BD交AC于点O．

∵ABCD为菱形，∠DAB＝60°，

∴∠OAB＝30°，∠AOB＝90°，AO＝CO．

∴AO＝AB×＝2×＝．

∴AC＝2．

故答案为：2．

（2）∵四边形ABCD是菱形，且菱形ABCD的边长为2cm，

∴AB＝BC＝2，∠BAC＝∠DAB，

又∵∠DAB＝60°（已知），

∴∠BAC＝∠BCA＝30°；

如图1，连接BD交AC于O．

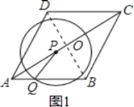
∵四边形ABCD是菱形，

∴AC⊥BD，OA＝AC，

∴OB＝AB＝1（30°角所对的直角边是斜边的一半），

∴OA＝（cm），AC＝2OA＝2（cm），

运动ts后，AP＝ t，AQ＝t，

∴= =，

又∵∠PAQ＝∠CAB，

∴△PAQ∽△CAB，

∴∠APQ＝∠ACB（相似三角形的对应角相等），

∴PQ∥BC（同位角相等，两直线平行）

（2）如图2，⊙P与BC切于点M，连接PM，则PM⊥BC．

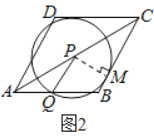
在Rt△CPM中，∵∠PCM＝30°，∴PM＝PC＝，由PM＝PQ＝AQ＝t，即＝t

解得t＝4﹣6，此时⊙P与边BC有一个公共点；

如图3，⊙P过点B，此时PQ＝PB，

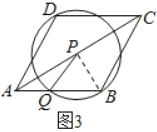
∵∠PQB＝∠PAQ+∠APQ＝60°

∴△PQB为等边三角形，∴QB＝PQ＝AQ＝t，∴t＝1

∴当4﹣6＜t≤1时，⊙P与边BC有2个公共点．

如图4，⊙P过点C，此时PC＝PQ，即2﹣t＝t，∴t＝3﹣．

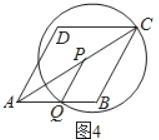
∴当1＜t≤3﹣时，⊙P与边BC有一个公共点，

当点P运动到点C，即t＝2时P与C重合，Q与B重合，也只有一个交点，此时，⊙P与边BC有一个公共点，

∴当t＝4﹣6或1＜t≤3﹣或t＝2时，⊙P与菱形ABCD的边BC有1个公共点；

当4﹣6＜t≤1时，⊙P与边BC有2个公共点．