题目内容
如图,△ABC是⊙O的内接三角形,AC是⊙O的直径,∠C=50°,∠ABC的平分线BD交⊙O于点D,则∠BAD的度数是( )
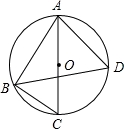
A.45° B.85° C.90° D.95°
B【考点】圆周角定理;圆心角、弧、弦的关系.
【分析】根据圆周角定理以及推论和角平分线的定义可分别求出∠BAC和∠CAD的度数,进而求出∠BAD的度数.
【解答】解:∵AC是⊙O的直径,
∴∠ABC=90°,
∵∠C=50°,
∴∠BAC=40°,
∵∠ABC的平分线BD交⊙O于点D,
∴∠ABD=∠DBC=45°,
∴∠CAD=∠DBC=45°,
∴∠BAD=∠BAC+∠CAD=40°+45°=85°,
故选:B.
【点评】本题考查的是圆周角定理,即在同圆或等圆中,同弧或等弧所对的圆周角相等,直径所对的圆周角是直角.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 都有意义的x的取值范围是__________.
都有意义的x的取值范围是__________. ,那么x的值是( )
,那么x的值是( ) B.
B. C.
C. D.
D.
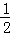 ,xn=
,xn= (n为不小于2的整数),则x2015= .
(n为不小于2的整数),则x2015= . ,求GC的长.
,求GC的长.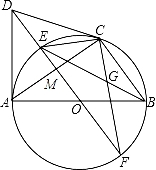
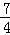 )2=
)2=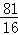 D.3x2﹣4x﹣2=0化为(x﹣
D.3x2﹣4x﹣2=0化为(x﹣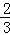 )2=
)2=