题目内容
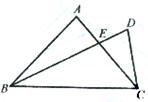 13、如图,已知在线段BC同侧作两个三角形△ABC和△DBC,使AB=AC,DB>DC且AB+AC=DB+DC,设AC与DB交于E.
13、如图,已知在线段BC同侧作两个三角形△ABC和△DBC,使AB=AC,DB>DC且AB+AC=DB+DC,设AC与DB交于E.求证:AE>DE.
分析:由已知可得BD>AC,在BD上截取DF=AC,连接AF、AD,根据三角形三边关系可得AF>CD,再由在两个三角形中,如果有两对应边分别相等,那么对边较大的,其夹角也较大,可得∠1>∠2,再根据大角对大边即可证明AE>DE.
解答: 证明:由已知可得2BD>BD+DC=AB+AC=2AC,
证明:由已知可得2BD>BD+DC=AB+AC=2AC,
∴BD>AC,
在BD上截取DF=AC,连接AF、AD(如图)
∵BD+DC=2AC,
∴DC+BF=AC+AB,
∴在△BAF中,AF>AB-BF=DC.
在△BAD与△ADF中,
AD=AD,AC=DF,AF>CD,
∴∠1>∠2,
∴AE>DE.
 证明:由已知可得2BD>BD+DC=AB+AC=2AC,
证明:由已知可得2BD>BD+DC=AB+AC=2AC,∴BD>AC,
在BD上截取DF=AC,连接AF、AD(如图)
∵BD+DC=2AC,
∴DC+BF=AC+AB,
∴在△BAF中,AF>AB-BF=DC.
在△BAD与△ADF中,
AD=AD,AC=DF,AF>CD,
∴∠1>∠2,
∴AE>DE.
点评:本题考查了三角形三边关系.解题的关键是作辅助线,构造有两对应边分别相等的两个三角形得出∠1>∠2.

练习册系列答案
相关题目
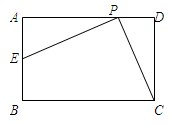 连接PC,过点P作PE⊥PC交AB于E
连接PC,过点P作PE⊥PC交AB于E 如图,已知在△ABC中,∠B=90°,AB=8cm,BC=6cm,点P开始从点A开始沿△ABC的边做逆时针运动,且速度为每秒1cm,点Q从点B开始沿△ABC的边做逆时针运动,且速度为每秒2cm,他们同时出发,设运动时间我t秒.
如图,已知在△ABC中,∠B=90°,AB=8cm,BC=6cm,点P开始从点A开始沿△ABC的边做逆时针运动,且速度为每秒1cm,点Q从点B开始沿△ABC的边做逆时针运动,且速度为每秒2cm,他们同时出发,设运动时间我t秒.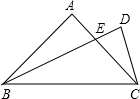 如图,已知在线段BC同侧作两个三角形△ABC和△DBC,使AB=AC,DB>DC且AB+AC=DB+DC,设AC与DB交于E.
如图,已知在线段BC同侧作两个三角形△ABC和△DBC,使AB=AC,DB>DC且AB+AC=DB+DC,设AC与DB交于E.