题目内容
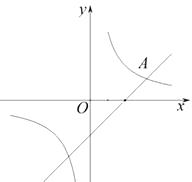
【题目】已知:如图,在平面直角坐标系xoy中,一次函数y= ![]() x+3的图象与x轴和y轴交于A、B两点,将△AOB绕点O顺时针旋转90°后得到△A′OB′.
x+3的图象与x轴和y轴交于A、B两点,将△AOB绕点O顺时针旋转90°后得到△A′OB′.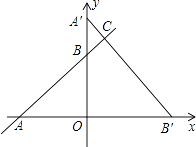
(1)求直线A′B′的解析式;
(2)若直线A′B′与直线AB相交于点C,求S△ABC:S△ABO的值.
【答案】
(1)解:根据y= ![]() x+3,解得点坐标A(﹣4,0),B(0,3),即OA=4,OB=3,
x+3,解得点坐标A(﹣4,0),B(0,3),即OA=4,OB=3,
∴OA′=OA=4,OB′=OB=3,
∴A′(0,4),B′(3,0),
设直线A′B′的解析式为y=kx+b,则 ![]() ,解得
,解得 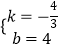 ,
,
∴直线A′B′的解析式为y=﹣ ![]() +4;
+4;
(2)解:解方程组  ,
,
求得两直线交点坐标,得C( ![]() ,
, ![]() ),
),
∴S△A′BC=1× ![]() =
= ![]() ,S△ABO=4×3×
,S△ABO=4×3× ![]() =6,
=6,
∴ ![]() =
= ![]() .
.
【解析】(1)抓住已知将△AOB绕点O顺时针旋转90°后得到△A′OB′.根据旋转的性质得出OA′=OA,OB′=OB,先求出直线AB与两坐标轴的交点坐标,即可得出点A′,B′的坐标,利用待定系数法就可以求出直线A′B′的解析式。
(2)先根据两函数解析式联立方程组,求出方程组的解,即点C的坐标,就可以求出△A′BC和△ABO的面积,即可求出它们的面积之比。
【考点精析】本题主要考查了确定一次函数的表达式和三角形的面积的相关知识点,需要掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;三角形的面积=1/2×底×高才能正确解答此题.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目