题目内容
【题目】综合题
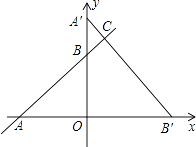
(1)如图1,△ABC中, ![]() ,AB的垂直平分线交AC于点D,连接BD.若AC=2,BC=1,则△BCD的周长为;
,AB的垂直平分线交AC于点D,连接BD.若AC=2,BC=1,则△BCD的周长为;
(2)O为正方形ABCD的中心,E为CD边上一点,F为AD边上一点,且△EDF的周长等于AD的长.
①在图2中求作△EDF(要求:尺规作图,不写作法,保留作图痕迹);
②在图3中补全图形,求 ![]() 的度数;
的度数;
③若 ![]() ,则
,则 ![]() 的值为 .
的值为 . 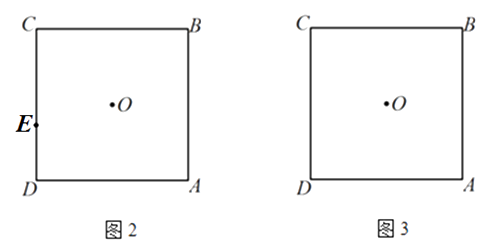
【答案】
(1)3
(2)解:①如图,△ ![]() 即为所求;
即为所求;  ,②在AD上截取AH,使得AH=DE,连接OA、OD、OH.
,②在AD上截取AH,使得AH=DE,连接OA、OD、OH. ∵点O为正方形ABCD的中心,∴
∵点O为正方形ABCD的中心,∴ ![]() ,
,![]() ,
,![]() .∴△
.∴△ ![]() ≌△
≌△ ![]() .∴
.∴ ![]() ,
,![]() .∴
.∴ ![]() .∵△
.∵△ ![]() 的周长等于
的周长等于 ![]() 的长,∴
的长,∴ ![]() .∴△
.∴△ ![]() ≌△
≌△ ![]() .∴
.∴ ![]() .,③
.,③ ![]() .
.
【解析】(1) ![]() AB的垂直平分线交AC于点D,
AB的垂直平分线交AC于点D,
∴BD=AD,
∴ ![]() BCD的周长=BC+CD+BD=BC+AC=1+2+3,
BCD的周长=BC+CD+BD=BC+AC=1+2+3,
所以答案是:3
( 2 )③作OG ![]() CD于G,OK
CD于G,OK ![]() AD于K,如图3所示:
AD于K,如图3所示:

设AF=8t,则CE=9t,设OG=m,
∵O为正方形ABVD的中心,
∴四边形OGDK为正方形,CG=DG=DK=KA= ![]() AB=OG,
AB=OG,
∴GE=CE-CG=9t-m,DE=2CG-CE=2m-9t,FK=AF-KA=8t-m,DF=2DK-AF=2m-8t,
由(2)②知 ![]() EOG ≌
EOG ≌ ![]() HOF,
HOF,
∴OE=OH,EF=FH,
在Rt ![]() EOG和Rt
EOG和Rt ![]() HOK中,
HOK中,
![]() ,
,
∴Rt ![]() EOG ≌Rt
EOG ≌Rt ![]() HOK(HL),
HOK(HL),
∴GE=KH,
∴EF=GE+FK=9t-m+8t-m=17t-2m,
由勾股定理得:DE2+DF2=EF2,
∴(2m-9t)2+(2m-8t)2=(17t-2m)2,
整理得:(m+6t)(m-6t)=0,
∴m=6t
∴OG=OK=6t,GE=9t-m=9t-6t=3t,FK=8t-m=2t,
∴ ![]()
所以答案是: ![]()
【考点精析】掌握比例的性质是解答本题的根本,需要知道基本性质;更比性质(交换比例的内项或外项);反比性质(交换比的前项、后项);等比性质.

【题目】如图所示,一张边长为![]() 的正方形硬纸板,把它的四个角都剪去一个边长为工
的正方形硬纸板,把它的四个角都剪去一个边长为工![]() (
(![]() 为正整数)的小正方形,然后把它折成一个无盖的长方体,设长方体的容积为
为正整数)的小正方形,然后把它折成一个无盖的长方体,设长方体的容积为![]() ,请回答下列问题:
,请回答下列问题:
(1)用含有![]() 的代数式表示
的代数式表示![]() ,则
,则![]()
(2)完成下表:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|
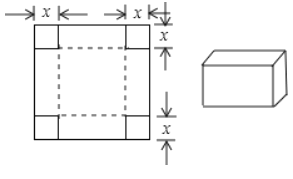
(3)观察上表,当![]() 取什么值时,容积
取什么值时,容积![]() 的值最大?
的值最大?