题目内容
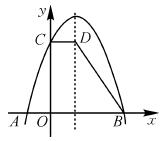
已知二次函数y=x2-4x+3.
(1)用配方法求其函数图象的顶点C的坐标，并描述该函数的函数值随自变量的增减而增减的情况；
(2)求函数图象与x轴的交点A，B的坐标，及△ABC的面积.
(1)y=x2-4x+3=(x-2)2-1.
∴其函数的顶点C的坐标为(2，-1)，
∴当x<2时，y随x的增大而减小；
当x>2时，y随x的增大而增大
.
(2)令y=0，则x2-4x+3=0,解得x1=1,x2=3.
∴当点A在点B左侧时，A(1，0)，B(3，0)；
当点A在点B右侧时，A(3，0)，
B(1，0).
∴AB=|1-3|=2.
过点C作CD⊥x轴于D，则
△ABC的面积=
AB·CD=×2×1=1.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
，则弹簧的总长度y(cm)与所挂物体质量x(kg)之间的函数关系式为y=10+0.5x(0≤x≤5).”王刚同学在阅读上面材料时发现部分内容被墨迹污染，被污染的部分是确定函数关系式的一个条件，你认为该条件可以是： (只需写出1个).
(k>0)的图象与矩形ABCO的两边相交于E、F两点.若E是AB的中点，S△BEF=2，则k的值为 .
m+1的图象与x轴只有一个交点，那么m的值为( )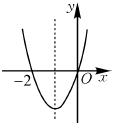
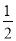）+（﹣12）+
；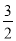