题目内容
6. 如图A,B,C,D在⊙O上,已知AB=10,CD=6,∠A+∠C=90°,则⊙O的半径=$\sqrt{34}$.
如图A,B,C,D在⊙O上,已知AB=10,CD=6,∠A+∠C=90°,则⊙O的半径=$\sqrt{34}$.
分析 延长AO交⊙O于点E,连接BE,根据三角形外角的性质可知∠BOE=∠A+∠B,再由∠A+∠C=90°可知∠A+∠B+∠C+∠D=180°,故∠DOC=∠A+∠B,故可得出△OCD≌△OBE,故BE=CD,再由勾股定理即可得出结论.
解答 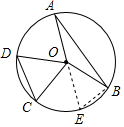 解:延长AO交⊙O于点E,连接BE,
解:延长AO交⊙O于点E,连接BE,
∵∠BOE是△AOB的外角,
∴∠BOE=∠A+∠B.
∵∠A+∠C=90°,∠C=∠D,∠A=∠B,
∴∠A+∠B+∠C+∠D=180°,
∴∠DOC=∠A+∠B,
∴∠DOC=∠BOE.
在△OCD与△OBE中,
∵$\left\{\begin{array}{l}{OC=OB}\\{∠DOC=∠BOE}\\{OD=OE}\end{array}\right.$,
∴△OCD≌△OBE(SAS),
∴BE=CD=6.
∵AE是⊙O的直径,
∴∠ABE=90°,
∴AE=$\sqrt{A{B}^{2}+B{E}^{2}}$=$\sqrt{1{0}^{2}+{6}^{2}}$=2$\sqrt{34}$,
∴⊙O的半径=$\sqrt{34}$.
故答案为:$\sqrt{34}$.
点评 本题考查的是圆周角定理,根据题意作出辅助线,构造出圆周角是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.计算:
| (1)-150+250; | (2)-15+(-23); |
| (3)-5-65; | (4)-26-(-15); |
| (5)-6×(-16); | (6)-$\frac{1}{3}$×27; |
| (7)8÷(-16); | (8)-25÷(-$\frac{2}{3}$); |
| (9)(-0.02)×(-20)×(-5)×4.5; | (10)(-6.5)×(-2)÷(-$\frac{1}{3}$)÷(-5); |
| (11)6+(-$\frac{1}{5}$)-2-(-1.5); | (12)-66×4-(-2.5)÷(-0.1); |
| (13)(-2)2×5-(-2)3÷4; | (14)-(3-5)+32×(1-3) |
 如图是将两个棱长为40mm的正方体分别切去一 块后剩下的余料,在它们的三视图中,完全相同的是俯视图和主视图.
如图是将两个棱长为40mm的正方体分别切去一 块后剩下的余料,在它们的三视图中,完全相同的是俯视图和主视图.
 如图,在△ABC中,∠C=90°,三角形的角平分线AD、BE相交于F,则∠AFB=135°.
如图,在△ABC中,∠C=90°,三角形的角平分线AD、BE相交于F,则∠AFB=135°.