题目内容
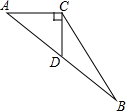
如图，在梯形ABCD中，AB∥CD，BC⊥CD，AD⊥BD，CD=4，sinA=
，求梯形ABCD的面积．
| 4 |
| 5 |
∵AB∥CD，BC⊥CD，AD⊥BD，
∴∠A+∠ABD=90°，∠DBC+∠ABD=90°．
∴∠A=∠DBC．（1分）
∴sin∠DBC=sinA=
．（1分）
在Rt△BCD中，BD=
=4×
=5．（2分）
BC=
=
=3．（1分）
在Rt△ABD中，AB=
=5×
=
．（1分）
∴S梯形=
×3×(4+
)=
．（1分）
∴∠A+∠ABD=90°，∠DBC+∠ABD=90°．
∴∠A=∠DBC．（1分）
∴sin∠DBC=sinA=
| 4 |
| 5 |
在Rt△BCD中，BD=
| CD |
| sin∠DBC |
| 5 |
| 4 |
BC=
| AB2-CD2 |
| 52-42 |
在Rt△ABD中，AB=
| BD |
| sinA |
| 5 |
| 4 |
| 25 |
| 4 |
∴S梯形=
| 1 |
| 2 |
| 25 |
| 4 |
| 123 |
| 8 |
练习册系列答案
阅读快车系列答案
相关题目
路径
