题目内容
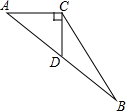
如图所示，在△ABC中，DC上AC交AB于点D，若S△ACD：S△CDB=2：3，cos∠DCB=
，求∠A的度数．
| 4 |
| 5 |
作DE⊥DC，交CB于点E，如图所示，
∵AC⊥CD，
∴DE∥AC，
在Rt△CDE中，cos∠DCB=
=
，
设CD=4x，CE=5x，则DE=3x，
∵S△ACD：S△CDB=2：3，△ACD与△CDB中AD、DB边上的高相等，
∴AD：DB=2：3，
∴DB：AB=3：5，
∵DE∥AC，
∴
=
=
，
∵DE=3x，
∴AC=5x，
在Rt△ACD中，tanA=
=
=
，
则∠A≈38°40′．
∵AC⊥CD，
∴DE∥AC，
在Rt△CDE中，cos∠DCB=
| 4 |
| 5 |
| CD |
| CE |
设CD=4x，CE=5x，则DE=3x，
∵S△ACD：S△CDB=2：3，△ACD与△CDB中AD、DB边上的高相等，
∴AD：DB=2：3，
∴DB：AB=3：5，
∵DE∥AC，
∴
| DE |
| AC |
| DB |
| AB |
| 3 |
| 5 |
∵DE=3x，
∴AC=5x，
在Rt△ACD中，tanA=
| CD |
| AC |
| 4x |
| 5x |
| 4 |
| 5 |
则∠A≈38°40′．
练习册系列答案
相关题目
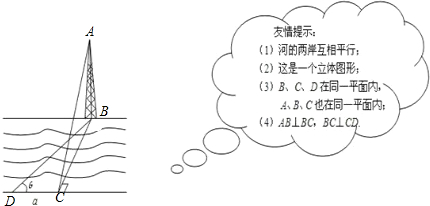
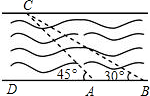学在点A处观测到对岸C点，测得∠CAD=45°，又在距A处60米远的B处测得∠CBA=30°，
DCFE，EF
