题目内容
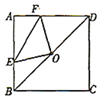
【题目】如图,在△ABC中,∠ACB=90°,O是AB上一点,以OA为半径的⊙O与BC相交于点D,与AB交于点E,AD平分∠FAB,连接ED并延长交AC的延长线于点F.
(1)求证:BC为⊙O的切线.
(2)求证:AE=AF;
(3)若DE=3,sin∠BDE=![]() ,求AC的长.
,求AC的长.
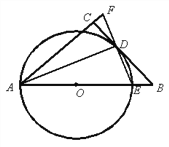
【答案】(1)证明见解析;(2)证明见解析;(3)AC= 8.
【解析】
(1)连接OD.证明OD⊥CB即可.
(2)根据切线的性质和平行线的性质解答即可;
(3)根据直角三角形的性质和三角函数解答即可.
(1)证明:连接OD.
∵AD平分∠FAB
∴∠CAD=∠DAB
在⊙O中,OA=OD
∠DAB=∠ODA
∴∠CAD=∠ODA
∴AC∥OD
∴∠ODB=∠ACB=900
∴OD⊥CB
∴CB为⊙O的切线
(2)证明∵ OD=OE,
∴∠ODE=∠OED.
∵直线BC为⊙O的切线,
∴OD⊥BC.
∴∠ODB=90°.
∵∠ACB=90°,
∴OD∥AC .
∴∠ODE=∠F.
∴∠OED=∠F.
∴AE=AF.
(3)∵AE是⊙O的直径
∴∠ADE=90°.
∵AE=AF,
∴DF=DE=3.
∵∠ACB=90°.
∴∠DAF+∠F=90°,∠CDF+∠F=90°,
∴∠DAF=∠CDF=∠BDE.
在Rt△ADF中,
![]() ,
,
∴![]() .
.
在Rt△CDF中,
![]() ,
,
∴![]() .
.
∴AC=AF-CF=8.

 一课一练课时达标系列答案
一课一练课时达标系列答案【题目】射阳县实验初中为了解全校学生上学期参加社区活动的情况,学校随机调查了本校50名学生参加社区活动的次数,并将调查所得的数据整理如下:
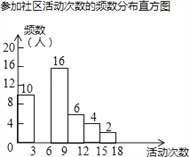
参加社区活动次数的频数、频率分布表
活动次数x | 频数 | 频率 |
0<x≤3 | 10 | 0.20 |
3<x≤6 | a | 0.24 |
6<x≤9 | 16 | 0.32 |
9<x≤12 | 6 | 0.12 |
12<x≤15 | m | b |
15<x≤18 | 2 | n |
根据以上图表信息,解答下列问题:
(1)表中a= ,b= ;
(2)请把频数分布直方图补充完整(画图后请标注相应的数据);
(3)若该校共有1200名学生,请估计该校在上学期参加社区活动超过6次的学生有多少人?