Question

【题目】如图，点在第二象限，其中，满足等式，点在第一象限内，射线，与轴交于点．

（1）当时，求点的坐标；

（2）点在轴上从出发以每秒1个单位长度的速度向点运动（到达点后停止运动），求当时间为秒时（不考虑点与点重合的情况），，，的大小关系；

（3）如图，若，点是射线上一动点，，的平分线交于点．的大小是否随点的位置变化发生改变，若不变，请求出的度数；若改变，说明理由．

Answer 1

【答案】（1）点的坐标为；（2）当时，；当时，，证明详见解析；（3）的大小不随点的位置变化发生改变，，理由见解析．

【解析】

（1）根据非负数的意义，可得方程组，进而求出a，b，确定点A的坐标；
（2）分两种情况，画出相应图象，根据两直线平行，同位角或内错角相等和三角形的一个外角等于与它不相邻的两个内角的和，可以得出这三个角的大小关系；

（3）根据两直线平行，同旁内角互补，可得，在根据角平分线的定义和三角形内角和定理可求出∠E是个定值．

解：（1），

又，，

，．

且．

当时，，．

∴a=-3，b=2，

点的坐标为；

（2）①当0＜t＜3时，即点P在y轴的负半轴移动时，如图2-1，此时∠AOP=∠OPB+∠PBC；

∵OA∥BC，
∴∠AOP=∠OCQ，
又∵∠OCQ=∠OPB+∠PBC，
∴∠AOP=∠OPB+∠PBC，

②当3＜t＜8时，即点P在OC上移动时，如图2-2，此时∠OPB=∠AOP+∠PBC，

∵OA∥BC，
∴∠AOP=∠PCB，
又∵∠OPB═∠PBC+∠BCP，
∴∠OPB=∠AOP+∠PBC；

（3）的大小不随点的位置变化发生改变，，

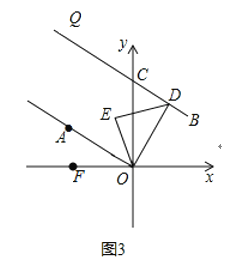
证明如下：

，

，

设，则，

，

平分，平分，

，

．