��Ŀ����
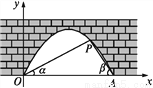
��ͼ������������,P����һ������,ˮ��OA��4 m,��O,A�����۲�P��,���Ƿֱ�Ϊ��,��,��tan ��=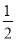 ,tan ��=
,tan ��=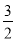 ,��OΪԭ��,OA����ֱ��Ϊx�Ὠ��ƽ��ֱ������ϵ.
,��OΪԭ��,OA����ֱ��Ϊx�Ὠ��ƽ��ֱ������ϵ.
(1)���P������.
(2)ˮ������1 m,ˮ�������?(�����ȷ��0.1 m.�ο�����: 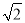 ��1.41)
��1.41)
��ϰ��ϵ�д�
 �Ƹ�С״Ԫ�������������ϵ�д�
�Ƹ�С״Ԫ�������������ϵ�д� ����һ������ܼƻ�ϵ�д�
����һ������ܼƻ�ϵ�д�
�����Ŀ
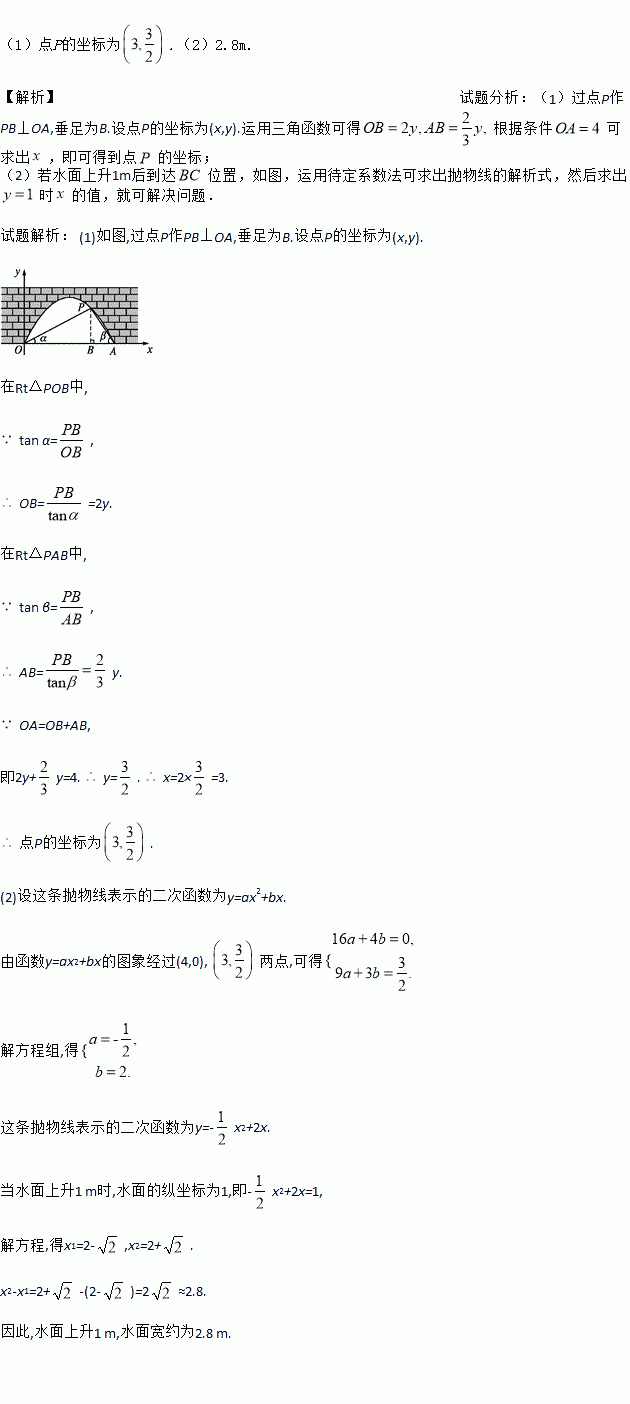

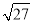 B.
B.  C.
C. 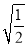 D.
D. 