题目内容
10.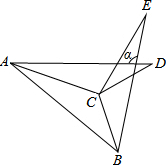 如图,△BCE和△ACD是由△ABC分别沿着BC、AC边翻折180°形成的,若∠ACB=130°,那么∠α的度数为100.
如图,△BCE和△ACD是由△ABC分别沿着BC、AC边翻折180°形成的,若∠ACB=130°,那么∠α的度数为100.
分析 根据轴对称的性质可得∠BAC=∠DAC,∠ABC=∠EBC,然后根据三角形的一个外角等于与它不相邻的两个内角的和表示出∠α,再根据三角形的内角和等于180°列式计算即可得解.
解答 解:∵△ACD和△BCE分别是△ACB的轴对称图形,
∴∠BAC=∠DAC,∠ABC=∠EBC,
由三角形的外角性质得,∠α=∠BAD+∠ABE,
=∠BAC+∠DAC+∠ABC+∠EBC,
=2(∠BAC+∠ABC),
∵∠ACB=130°,
∴∠BAC+∠ABC=180°-130°=50°,
∴∠α=2×50°=100°.
故答案为:100°.
点评 本题考查轴对称的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,三角形的内角和定理,熟记性质并表示出∠α是解题的关键.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
14.下列图形是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
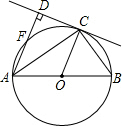 如图,AB为⊙O的直径,OC为⊙O的半径,AD⊥DC于D,AC平分∠DAB,AD交⊙O于点E.
如图,AB为⊙O的直径,OC为⊙O的半径,AD⊥DC于D,AC平分∠DAB,AD交⊙O于点E.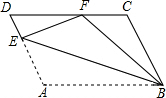 如图,在?ABCD中,E为AD上一点,以BE为折痕将△ABE向上翻折,点A恰好落在CD上的点F处.若△FDE的周长为12,△FCB的周长为22,则FC的长为5.
如图,在?ABCD中,E为AD上一点,以BE为折痕将△ABE向上翻折,点A恰好落在CD上的点F处.若△FDE的周长为12,△FCB的周长为22,则FC的长为5.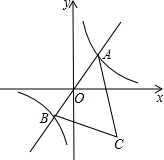 如图,已知A是双曲线y=$\frac{7}{x}$在第一象限的分支上一个动点,连接AO并延长另一分支于点B,以AB为一边作等边△ABC,点C在第四象限,随着点A的运动,点C的位置也不断发生变化,但点C始终在双曲线y=$\frac{k}{x}$(k<0)上运动,则k的值是-21.
如图,已知A是双曲线y=$\frac{7}{x}$在第一象限的分支上一个动点,连接AO并延长另一分支于点B,以AB为一边作等边△ABC,点C在第四象限,随着点A的运动,点C的位置也不断发生变化,但点C始终在双曲线y=$\frac{k}{x}$(k<0)上运动,则k的值是-21.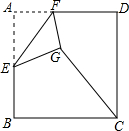 如图,在边长为2的正方形ABCD中,E是AB的中点,F是AD边上的一个动点,将△AEF沿EF所在直线折叠得到△GEF,连接GC,则GC长度的最小值是$\sqrt{5}$-1.
如图,在边长为2的正方形ABCD中,E是AB的中点,F是AD边上的一个动点,将△AEF沿EF所在直线折叠得到△GEF,连接GC,则GC长度的最小值是$\sqrt{5}$-1.