题目内容
2. 如图,已知:DE∥BC,AB∥DF.
如图,已知:DE∥BC,AB∥DF.(1)求i正:OB2=OE•OF;
(2)联结OD,若∠OBC=∠ODC,求证:四边形ABCD是菱形.
分析 (2)由平行线分线段成比例定理,即可证得OB2=OE•OF;
(3)连接BD,交AC于点H,先证明四边形ABCD是平行四边形,再证得△ODF∽△OED,即可证得OD2=OE•OF,则得到OB=OD,又由OH⊥BD,即可证得四边形ABCD为菱形.
解答 (1)证明:∵DE∥BC,AB∥DF,
∴$\frac{OB}{OE}=\frac{OC}{OA}$,$\frac{OF}{OB}=\frac{OC}{OA}$,
∴$\frac{OB}{OE}=\frac{OF}{OB}$,
∴OB2=OE•OF;
(2)证明:连接OD,连接BD,交AC于点H,如图所示:
∵DE∥BC,AB∥DF,
∴四边形ABCD是平行四边形,∠OBC=∠E,
∴BH=DH,
∵∠OBC=∠ODC,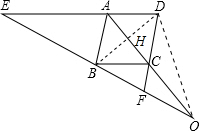
∴∠ODC=∠E,
∵∠DOF=∠DOE,
∴△ODF∽△OED,
∴$\frac{OD}{OE}=\frac{OF}{OD}$,
∴OD2=OE•OF,
∵OB2=OF•OE,
∴OB=OD,
∵平行四边形ABCD中,BH=DH,
∴OH⊥BD,
∴四边形ABCD为菱形.
点评 此题考查了相似三角形的判定与性质,平行四边形的性质,菱形的判定以及平行线分线段成比例定理等.综合性很强,图形较复杂,解题时要注意识图,灵活应用数形结合思想.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
13.若等腰三角形的两边长分别为2和5,则它的周长为( )
| A. | 9 | B. | 7 | C. | 12 | D. | 9或12 |
10.方程组$\left\{\begin{array}{l}{x-1=0}\\{x+y=0}\end{array}\right.$的解是( )
| A. | $\left\{\begin{array}{l}{x=1}\\{y=-2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=-1}\\{y=4}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=1}\\{y=0}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=3}\\{y=-2}\end{array}\right.$ |
17.在数轴上表示-3的点与表示3的点之间的距离是( )
| A. | 6 | B. | -6 | C. | 0 | D. | -1 |
7. 如图,点E在BC延长线上,下列条件中,不能推断AB∥CD的是( )
如图,点E在BC延长线上,下列条件中,不能推断AB∥CD的是( )
 如图,点E在BC延长线上,下列条件中,不能推断AB∥CD的是( )
如图,点E在BC延长线上,下列条件中,不能推断AB∥CD的是( )| A. | ∠4=∠3 | B. | ∠1=∠2 | C. | ∠B=∠5 | D. | ∠B+∠BCD=180° |
14. 如图,在矩形ABCD中,对角线AC、BD交于点O,AE⊥BD于E,BE=EO=1,则BC的长为( )
如图,在矩形ABCD中,对角线AC、BD交于点O,AE⊥BD于E,BE=EO=1,则BC的长为( )
 如图,在矩形ABCD中,对角线AC、BD交于点O,AE⊥BD于E,BE=EO=1,则BC的长为( )
如图,在矩形ABCD中,对角线AC、BD交于点O,AE⊥BD于E,BE=EO=1,则BC的长为( )| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | $2\sqrt{5}$ | D. | 4 |
10.下列运算中结果正确的是( )
| A. | a3•a2=a6 | B. | 3x2+2x2=5x4 | C. | (2x2)3=6x6 | D. | a10÷a9=a |
9.在下列实数中,-3,$\sqrt{2}$,0,2,-1中,绝对值最小的数是( )
| A. | -3 | B. | 0 | C. | $\sqrt{2}$ | D. | -1 |
 如图所示的几何体是一个由圆柱体和一个长方体组成的立体图形,从上面看=观察这个立体图形,能得到的平面图形是( )
如图所示的几何体是一个由圆柱体和一个长方体组成的立体图形,从上面看=观察这个立体图形,能得到的平面图形是( )


