题目内容
20.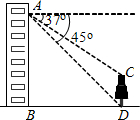 如图,小林在自家楼房的窗户A处,测量楼前的一棵树CD的高.现测得树顶C处的俯角为37°,树底D处的俯角为45°,测试点A的高度AB为20米.请你帮助小林计算树的高度(精确到0.1米).
如图,小林在自家楼房的窗户A处,测量楼前的一棵树CD的高.现测得树顶C处的俯角为37°,树底D处的俯角为45°,测试点A的高度AB为20米.请你帮助小林计算树的高度(精确到0.1米).(参考数据:sin37°≈0.602,cos37°≈0.799,tan37°≈0.754)
分析 过点C作CE垂直点A所在的水平线于点E,则在图中得到两个直角三角形,利用三角函数定义分别计算出ED和EC,求差即可.
解答 解:过点C作CE垂直点A所在的水平线于点E,则CE⊥AE,
在Rt△ADE中,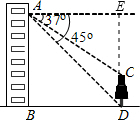
∵∠AED=90°,∠EAD=45°,
∴∠ADE=45°=∠EAD,
∴AE=DE=AB=20,
在Rt△ACE中,
∵∠AED=90°,∠EAC=37°,
∴tan∠EAC=$\frac{CE}{AE}$,
∴CE=AE•tan37°≈20×0.754≈15.1,
∴CD=ED-CE=4.9(米).
答:树的高度约为4.9米.
点评 本题考查了解直角三角形的应用,解答本题的关键是借助俯角构造直角三角形,并结合图形利用三角函数解直角三角形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.若a为方程x2-x-5=0的解,则a-a2+1的值是( )
| A. | -6 | B. | 6 | C. | -4 | D. | 4 |
12.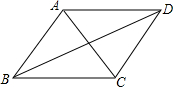 如图,下列条件之一能使平行四边形ABCD是菱形的为( )
如图,下列条件之一能使平行四边形ABCD是菱形的为( )
①AC⊥BD;②∠BAD=90°;③AB=BC;④AC=BD.
 如图,下列条件之一能使平行四边形ABCD是菱形的为( )
如图,下列条件之一能使平行四边形ABCD是菱形的为( )①AC⊥BD;②∠BAD=90°;③AB=BC;④AC=BD.
| A. | ①③ | B. | ②③ | C. | ③④ | D. | ①②③ |
 如图,把手机放在一个支架上面,就可以非常方便地使用,这是因为手机支架利用了三角形的稳定性.
如图,把手机放在一个支架上面,就可以非常方便地使用,这是因为手机支架利用了三角形的稳定性.