题目内容
17.若关于x、y的二元一次方程组$\left\{{\begin{array}{l}{3x-y=2a-5}\\{x+2y=3a+3}\end{array}}\right.$的解x是负数,y为正数.(1)求a的取值范围;
(2)化简2|a+2|+|2a-3|.
分析 (1)首先利用含a的式子表示x、y,再根据x<0,y>0,可得不等式组$\left\{{\begin{array}{l}{a-1<0}\\{a+2>0}\end{array}}\right.$,再解不等式组,确定a的取值范围即可;
(2)根据a的取值范围去绝对值然后再合并同类项即可.
解答 解:(1)解方程组得:$\left\{{\begin{array}{l}{x=a-1}\\{y=a+2}\end{array}}\right.$,
∵x<0,y>0,
∴$\left\{{\begin{array}{l}{a-1<0}\\{a+2>0}\end{array}}\right.$,
∴-2<a<1;
(2)∵-2<a<1,
∴原式=2(a+2)+3-2a=7.
点评 此题主要考查了二元一次方程组、一元一次不等式组的解法,以及绝对值的性质,关键是正确利用含a的式子表示x、y.

练习册系列答案
相关题目
7.对于条形统计图、折线统计图和扇形统计图这三种常见的统计图,下列说法正确的是( )
| A. | 通常不可互相转换 | |
| B. | 扇形统计图能清楚地表示出各部分在总体中所占的百分比 | |
| C. | 折线统计图能清楚地表示出每个项目的具体数目 | |
| D. | 条形统计图能清楚地反映事物的变化情况 |
5.某市2017年有25000名学生参加中考,为了了解这25000名考生的中考成绩,从中抽取了1000名考生的成绩进行分析,以下说法正确的是( )
| A. | 25000名考生是总体 | B. | 每名考生的成绩是个体 | ||
| C. | 1000名考生是总体的一个样本 | D. | 样本容量是25000 |
12.甲、乙两城市为了解决空气质量污染问题,对城市及其周边的环境污染进行了综合治理.在治理的过程中,环保部门每月初对两城市的空气质量进行监测,连续10个月的空气污染指数如图所示.其中,空气污染指数≤50时,空气质量为优;50<空气污染指数≤100时,空气质量为良;100<空气污染指数≤150时,空气质量为轻微污染.

(1)填写下表:
(2)从以下四个方面对甲、乙两城市的空气质量进行分析.
①从平均数和空气质量为优的次数来分析甲乙两城市的空气质量哪个好一些;
②从平均数和中位数来分析甲乙两城市的空气质量哪个好一些;
③从平均数和方差来分析甲乙两城市的空气质量变化情况;
④根据折线图上两城市空气污染指数的走势来分析甲乙两城市的空气质量哪个好一些.

(1)填写下表:
| 平均数 | 方差 | 中位数 | 空气质量为优的次数 | |
| 甲 | 80 | 340 | 85 | 1 |
| 乙 | 80 | 1060 | 80 | 3 |
①从平均数和空气质量为优的次数来分析甲乙两城市的空气质量哪个好一些;
②从平均数和中位数来分析甲乙两城市的空气质量哪个好一些;
③从平均数和方差来分析甲乙两城市的空气质量变化情况;
④根据折线图上两城市空气污染指数的走势来分析甲乙两城市的空气质量哪个好一些.
2.△ABC中,∠C=80°,∠A-∠B=20°,则∠A的度数是( )
| A. | 60° | B. | 40° | C. | 30° | D. | 20° |
6.下列计算正确的是( )
| A. | (ab)2=a2b2 | B. | 2(a+1)=2a+1 | C. | a2+a3=a6 | D. | a6÷a2=a3 |
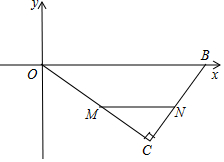 已知:如图所示,在平面直角坐标系xOy中,∠C=90°,OB=25,OC=20,若点M是边OC上的一个动点(与点O、C不重合),过点M作MN∥OB交BC于点N.
已知:如图所示,在平面直角坐标系xOy中,∠C=90°,OB=25,OC=20,若点M是边OC上的一个动点(与点O、C不重合),过点M作MN∥OB交BC于点N.